يمكن تقسيم المواد الموجودة الى نوعين :
1. المواد الصلبة Solid Matters.
2. المواد المائعة Fluid Matters.
أما المواد المائعة فتقسم الى قسمين هما:
1. المواد السائلة Liquid Matters.
2. المواد المائعة Gaseous Matters.
أن وجود المواد في أي من الحالات المذكورة أعلاه ووجود التشابه أو عدم وجوده بينهما يعود بصورة عامة الى نشاط Activity وتركيب Structure الجزيئات للمادة ويعتمد أيضاً على المسافة بين هذه الجزيئات ، ففي المواد الغازية تكون المسافة بين الجزيئات كبيرة نسبياً الى حجمها وتصبح صغيرة في المواد الصلبة والسائلة وأن نشاط جزيئات الغاز أكبر إذا ما قورن بنشاط جزيئات المواد الصلبة والسائلة وعليه نرى التماسك بين جزيئات المواد الصلبة كبيرة ، وحركة الجزيئات نسبة ً لبعضها البعض معدومة تقريباً.
وتزداد الحركة بين الجزيئات ويقل تماسكها نسبياً في المواد السائلة بينما نجد حركة جزيئات المواد الغازية كبيرة وتماسكها قليل ، لذا نرى الغازات تملأ الوعاء الذي يحويها ولكن السائل يملأ جزءاً من الوعاء ويأخذ شكله ويكون له سطح مستو حر ويفرض عادة ً عدم وجود فراغات داخل هذا الحجم وتكون هذه الفرضية مقبولة في التحليلات المختلفة.
والمواد الصلبة تتميز بالمرونة أي لها القابلية على الأنضغاط أما السوائل فأن قابليتها الأنضغاطية Compressibility قليلة ناتجة عن التماسك بين جزيئاتها ، وما يميز الموائع عن المواد الصلبة أنها لا تقاوم أجهاد القص Shear Stress مهما كان صغيراً عندما يكون في حالة السكون لأنه ينحرف ويحصل الجريان Flow
لذلك يمكن أن نعرّف المائع:
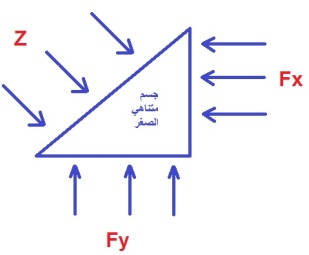
الجسم الذي يتغير شكله وينحرف بأقل قدر من قوة القص ويستمر بالتحرف ما دامت قوة القص واقعة عليه ، لذلك فالمائع في حالة السكون لا يكون فيه قوى قص وأن اي قوة واقعة على أي سطح حقيقي أو وهمي من مائع بحالة ركود لا بد أن تكون عمودية لذلك السطح وإذا لم تكن كذلك كانت لها محصلتان أحداهما عمودية والأخرى موازية له ، عند ذلك تسبب المحصلة الموازية قصاً ينتج عنه حركة تتنافى في حالة الركود المفترضة ومن مميزات المائع قابليته على نقل الضغط الواقع عليه الى جميع نقاطه وفي جميع الأتجاهات بالتساوي. وكذلك يقبل الأنضغاطية ولكنه لا يتحمل الشد إلا بقدر ضئيل جداً.
خواص الموائع :
وتطلق على الصفات الثابتة في الموائع التي لا تتغير في الأحوال الأعتيادية من نقطة الى أخرى ومن حين لآخر وتشمل:
1. الكثافة الكتلية Mass Density :
وهي كتلة وحدة الحجوم ، ووحداتها الأساسية بالنظام الفرنسي هي (كغم/م3) ، والكثافة الكتلية للجسم لا تتغير بتغيير النظام الجانبي وتبقى ثابتة في حال ثبوت درجة الحرارة والضغط ، وتدعى بالكثافة أختصاراً. ويرمز لها بـ (ρ).
2. الكثافة الوزنية Weight Density :
وهي وزن وحدة الحجوم ، أي قوة الجذب الأرضي ، ووحدة قياسها (نيوتن/م2) ويرمز لها بـ (ץ) ، وتتغير بتغير النظام الجاذبي Gravitational System ويمكن التعبير عن العلاقة بين الكثافتين بالمعادلة:
ץ = ρ. g
3. الكثافة النسبية Relative Density :
هي النسبة بين كثافة المادة وكثافة الماء في درجة حرارة 4 مئوية حيث يبلغ الماء كثافته العظمى تحت الضغط الجوي الاعتيادي.
4. الحجم النوعي Specific Volume :
وهو مقلوب الكثافة الكتلية (حجم / كتلة) ووحداتها م3/كغم ، ويرمز له بالحرف (V).
5. الانضغاطية Compressibility :
هي قابلية حجم المائع للتغير بتأثير القوى الخارجية الواقعة عليه. فالسائل ليس له القابلية على الأنضغاطية Incompressible fluid ، أما الغاز فله القابلية على الأنضغاط وتغيير حجمه Compressible Fluid والسبب يعود الى المسافات الموجودة بين جزيئات المائع نفسه.
6. اللزوجة Viscosity :
هي المقاومة التي تبديها طبقات المائع الى القوة القصية Shear Stress ، أن جميع الموائع في الطبيعة لها لزوجة ناتجة من تماسك جزيئاتها ومن تبادل الزخم بين طبقات المائع المختلفة الأرتفاعات وهذه الموائع تسمى بالموائع الحقيقية أو الموائع المختلفة الأرتفاعات وهذه الموائع تسمى بالموائع الحقيقية أو الموائع اللزجة Viscous Fluids حيث يكون بين طبقاتها أحتكاك عند الجريان وفيها تحصل حالتان للجريان:
(1) الجريان الهاديء أو الطبقي Laminar Flow : وفيه لا يحدث أمتزاج.
(2) الجريان المضطرب Turbulent Flow : وفيه يحدث أمتزاج دوامي بين طبقات المائع.
أما الموائع المثالية Ideal Fluids فليس لها لزوجة فهي غير موجودة في الطبيعة إلا أن قسماً من الموائع لزوجتها صغيرة جداً لدرجة أنها تهمل في الحسابات
واللزوجة على أنواع:
أ. اللزوجة الديناميكية Dynamic Viscosity: تعرّف بأنها النسبة بين أجهاد القص J ومنحدر السرعة (تغير السرعة/ تغير المسافة) ، وتقاس بـ (بويز Poise) حيث أن:
Poise = gm/m.sec
ب. اللزوجة الكينماتيكية Kinamatic Viscosity : نسبة اللزوجة الديناميكية / الكثافة الكتلية وتقاس بـ(ستوك Stock = cm2/sec) ويرمز لها بالرمز (ʯ) وكما يلي:
ʯ = Dynamic Viscosity / ρ
أن اللزوجة هي الأساس في مقارنة الموائع ، ولدرجة الحرارة أثر كبير في تغير قيمة اللزوجة لأن لزوجتها تختلف بأختلاف درجة الحرارة والسبب يعود الى طبيعة اللزوجة الناتجة من تماسك الجزيئات بعضها ببعض ومن تبادل الزخم بين طبقات المائع المختلفة الأرتفاعات فعند أرتفاع درجات الحرارة يزداد تبادل الزخم بين الطبقات بنسبة أكبر من النقصان الحاصل من تماسك الجزيئات ويحصل العكس في السوائل لذلك نرى أنخفاض اللزوجة عند أرتفاع درجة الحرارة تقل اللزوجة في السوائل وتزيد في الغازات.
أما الكميات التي تتغير من نقطة الى اخرى أو من حين الى آخر وهذه تطلق على خواص الجريان ، ومنها:
1 . السرعة Velocity : وهي كمية موجهة أي أن لها مقداراً وأتجاهاً وتعرف على أنها معدل المسافة المزاحة بالنسبة للزمن ووحدة قياسها m/sec . أي أن أبعادها متر
على ثانية.
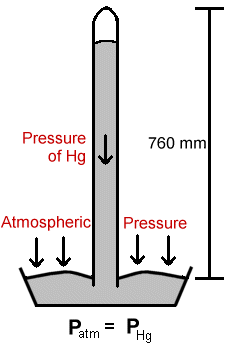
2 . الضغط Pressure : وهو القوة مقسومة على المساحة ووحدة قياسه النيوتن على المتر المربع N/m2 أو الباسكال Pascal ويرمز لها Pa ، ويوجد الضغط في جميع نقاط المائع تحت ضغط سواء أكان المائع في حالة سكون أو مائع ، والضغوط كمية غير موجهة لوقوعه من جميع الجهات على نقطة في المائع.
3 . القص Shear : وهو الأجهاد الناتج عن قوة تسبب الأنزلاق في جزء من المائع بالنسبة الى جزء آخر منه بأتجاه مواز لسطح تماسهما فهو كمية موجهة لها ، مقدار وأتجاهه خلافاً للضغط ويساوي القص قوة القص الكلي مقسوماً على المساحة ووحدة قياسه N/m2 أي الباسكال.
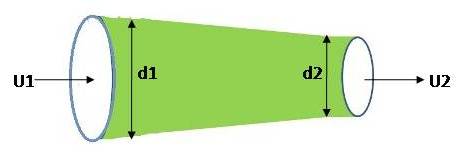
4 . التصريف Discharge : وهو كمية المائع الجاري في وحدة الزمن عبر المقطع في مجرى ويقاس في الموائع المنضغطة كالهواء والغازات بالقوة (الثقل في وحدة الزمن) فتكون وحدة قياسه N/sec ، أما في السوائل مثل الماء فيقاس بالحجم في وحدة الزمن ووحدة قياسه م3/ثانية ، وهو كمية غير موجهة وتقاس بمقدارها فقط.
5 . القوة Force : وهي كل ما ينتج أو يحاول أن ينتج أو يوقف أو يغير حركته وهي كمية موجهة ووحداتها النيوتن N ، وقد تستعمل معها وحدة الداين Dyne وهي جزء من 100 ألف جزء من النيوتن.
6 . الزمن Time : وهو المدة بين لحظتين ويرمز له بالحرف t وهو كمية غير موجهة ووحدته الأساسية هي الثانية sec .
7 . التعجيل Acceleration : ورمزه a وهو كمية موجهة ويعرف بأنه معدل تغير السرعة في وحدة الزمن ووحدة قياسه m/sec2 .