بسم الله الرحمن الرحيم
الحمد لله رب العالمين، والصلاة والسلام على أشرف الخلق والمرسلين، نبينا محمد، وعلى آله وصحبه الطيبين الطاهرين، أما بعد:
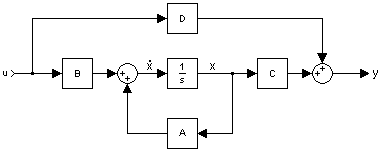
هذا هو الدرس الرابع من هذه السلسلة المباركة -إن شاء الله تعالى-، وسنتطرق في هذا الدرس إلى موضوع مهم جداً من المواضيع الأساسية في مادة التحكم وهو ما يسمى (State Space Representation)، وهو شكل آخر من أشكال المعادلات التفاضلية.
التمثيل المصفوفي للمعادلات التفاضلية (State Space Representation)
عند كتابة النموذج الرياضي Mathematical Model للنظام الفيزيائي، يبتدأ الشخص عادة بكتابة المعادلات التفاضلية. ولكن من الأفضل أن يعيد الشخص كتابة هذه المعادلات كدرجة أولى من المعادلات التفاضلية للأنظمة المختلفة، من حيث الحسابات ومن حيث عمل Simulation. وسنسمي هذا التمثيل للمعادلات التفاضلية بالتمثيل المصفوفي State Space Representation.
وحل هذا النوع من التمثيل للأنظمة يكون عبارة عن متجه Vector، ويعتمد هذا المتجه على الزمن، ويحتوي معلومات كافية للحصول بشكل كامل على مسير وكيفية عمل Trajectory هذا النظام الميكانيكي.
هذا المتجه يعود على حالة النظام State، ومكونات هذا المتجه تدعى عادة State Variables. لتوضيح هذه المفاهيم، سنطبق المثال التالي:
مثال: Spring-mass-damper system
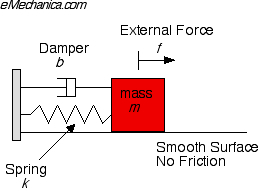
هذا هو نفس المثال الذي تمت مناقشته في الدرس الثاني، وقد قمنا باشتقاق المعادلة التفاضلية لهذا النظام. والمعادلة (انظر معادلة رقم2 في الدرس الثاني) هي:
![]()
لنعتبر أن المدخل لهذا النظام هو (f) والمُخْرَجْ (x). في هذا الحالة، لدينا معادلة تفاضلية من الدرجة الثانية، وهذا يعني أننا نحتاج إلى حالتين ابتدائيتين initial conditions لحل هذه المعادلة بشكل فريد (الحل الوحيد).
على سبيل المثال، تحديد قيم x(t0) وتحديد قيم dx/dt(t0) سيسمح بحل المعادلة x(t) للزمن t<t0.
لذلك نحتاج إلى متغيرين State Variables لوصف هذا النظام. وسنسمي (State Variables) ب xi، حيث i=1,2 ونقوم بعمل تحديد لهما.
![]()
سنقوم الآن بإعادة كتابة المعادلة التفاضلية في الأعلى بشكل مرتبط في State Variable، وسينتج لدينا ما يلي:
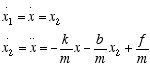
والآن نستطيع أن نستعمل المصفوفات لكتابة التمثيل المصفوفي للمعادلات التفاضلية State Space Representation:
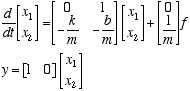
من المثال السابق، State Vector سيأخذ هذا الشكل:
![]()