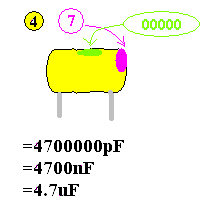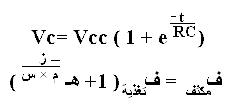تصميم الدوائر الإلكترونية

الهندسة الكهربائية الإلكترونيات والتحكم
1

شرح الدوائر الإلكترونية و تصميمها

سنحاول فى هذه السلسلة السير خطوة بخطوة نحو معرفة كيف تصمم الدوائر الإلكترونية ، الأمر خبرة لا تلقن بسهولة فى كلمات وهى أيضا كأى شيء آخر هبة يختلف فيها الأفراد ولكن بالتأكيد الشرح التالى قد يفيد.

إن لم تكن لديك الرغبة فى تصميم دائرة من البداية فعلى الأقل ستتمكن من تحليل دوائر الآخرين وهو ما لا غنى عنه للصيانة.

تصميم دائرة ككتابة مقال ، ولكى نكتب يجب أن نتعلم أولا اللغة – الحروف أولا ثم الكلمات ثم نكتب بعد ذلك.

الحروف هى

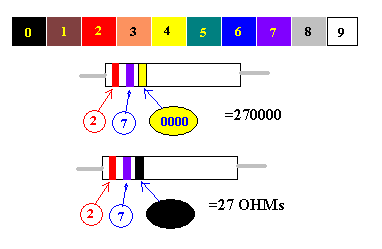
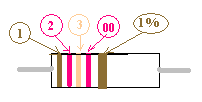
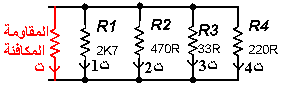
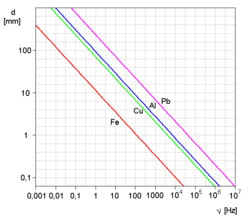
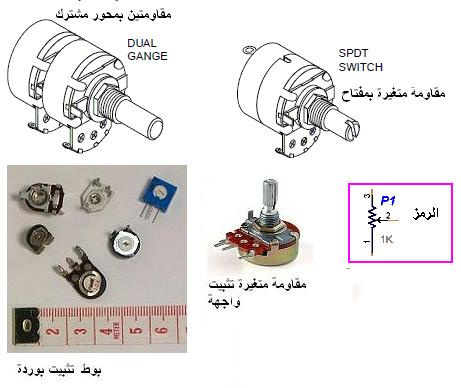
المقاومات بأنواعها
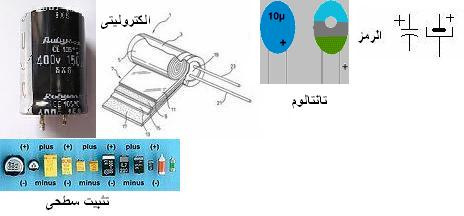
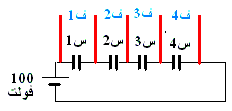
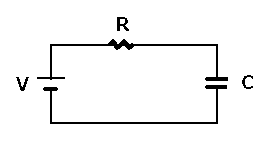
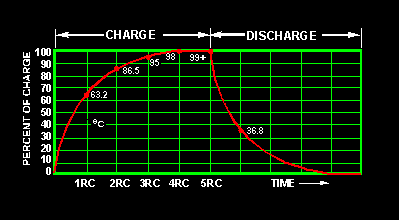
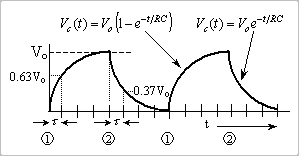
المكثفات بأنواعها
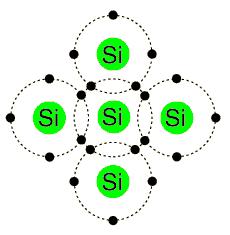
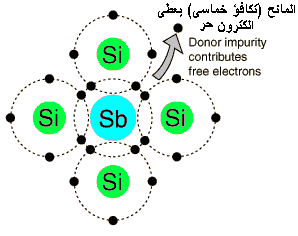
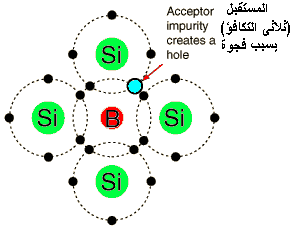
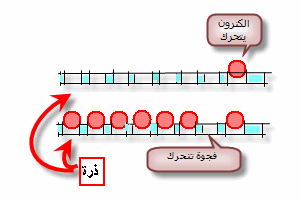
الدايودات بأنواعها
الترانزستورات بأنواعها

كما أن هناك جمل بليغة وتشبيهات يمكن اقتباسها فى المقالات نجد الأنواع التالية مثل
الدوائر الرقمية بأنواعها (بوابات-عدادات الخ) و يجب أن تعرف الوظائف المتاحة فى كل عائلة
الدوائر المتكاملة بأنواعها مثلا مكبرات العمليات مثل 741 و المؤقتات مثل 555 و مثبتات الجهد مثل مجموعة 7800 ، 7900 ، 317 الخ ، نوع من كل مجموعة وليس بالضرورة بالتفصيل و إنما يمكنك دائما اللجوء لكتب البيانات Data sheet لمعرفة التفاصيل أو اللجوء لمواقعها المتعددة ومن أفضلها

http://www.datasheetspdf.com/
http://www.datasheet4u.com

كما أن الحروف لا معنى لها فالمكونات السابقة ليس لها استخدام منفردة فيلزم مقاومتان على الأقل للحصول على مجزئ جهد أو مقاومة ومكثف لعمل مرشح ترددات.

لنتعلم الكلمات يجب أن نعرف كيف نجمع هذه “الحروف” لتكون مكبر ترانزيستور أو باستخدام LM741 أو دائرة توقيت 555 أو مولد ذبذبات هارتلى أو كولبتز وهى كلها دوائر تقليدية وموجودة بالكتب الأساسية لمقررات الإلكترونيات وما الفرق بين مكبر ترددات الصوت والترددات الأعلى كالفيديو ، أيضا بين تكبير الجهد وتكبير القدرة.

كما نختار و نرتب الكلمات لنركب جملة مفيدة نختار و نرتب الوحدات السابقة لنركب دائرة صغيرة تؤدى وظيفة محدودة وهنا تأتى الخبرة وكما يمكن أن يقول شخصا ما جملة طويلة بالكاد تستطيع فهمها وآخر يستخدم ما قل و دل يمكن أن يبنى شخصا دائرة كبيرة لعمل وظيفة صغيرة وآخر يعمل أخرى مختصرة تؤدى نفس الوظيفة – بل أفضل.

لذا يجب أن نذكر هنا أنه لا يوجد تصميم خطأ – ما دام قد أدى المهمة ولكن هناك تصميم أكفأ.

من المهم أن نقتبس هنا من مصممى أجهزة الفضاء “كل مكون يضاف – هو احتمال وارد للتلف والخطأ”.

و كما أن من الجمل تتكون الفقرات ومن الفقرات تتكون المقالات والكتب فمن الدائرة الصغيرة تتكون الدائرة الأكبر ومنها تتكون الدوائر المتراكبة.

هذا الأسلوب يسهل المرحلة التالية فى حال عدم أداء الدائرة المطلوب منها لأنك تعلم كل كلمة (دائرة اصغر) على حدة - ما دورها و يمكنك اختبارها لتحدد أين خرج الأداء عن المتوقع.

حال الدنيا أنه غالبا لا شيء يأتى من المرة الأولى فالخبرة غذاؤها الصبر و ماؤها المثابرة وبالتكرار تستطيع التطور.

كما أنك بتعلمك الكلمات تقرأ ما كتبه الآخرون وتتعلم منه البلاغة - بتعلمك هذه الوحدات تستطيع أن تحلل (تقرأ) دوائر الآخرين وتتعلم منها الحرفية والإتقان.

وكما أنك تقرأ للآخرين تشعر أن بها زيادات رغم كبر الاسم ، ستجد فى دوائر الآخرين مثل ذلك رغم كبر العلامة التجارية فالكثير منها يلجأ لحديث التخرج وفرا للنفقات ويركن للحاسبات لتعويض ذلك فالحاسب يشترى مرة واحدة ومن يعمل علية يتقاضى كل شهر ، لا تنظر للدوائر أنها كلام منزل ولكن حكم عقلك أولا ثم إن غلبك الفهم - اسأل.

و لسنا جميعا طه حسين أو العقاد أو شكسبير ولكن يكفى أن نكتب رسالة جيدة أو تقرير لنحل به ظرف ما - و أيضا ربما لن نصمم كلنا دوائر لأبحاث الفضاء ولكن نصنع شيئا أو نطور ما لدينا خير من أن نقف عاجزين أو نسأل أريد دائرة تعمل كذا – ثم لا نعرف فيم أخطأنا عند التجميع.

وختاما لا شيء يأتى مرة واحدة ولا علم يوضع فى كتاب واحد ولا خبرة تكفيها تجربة واحدة وتمنياتى للجميع بالتوفيق.

رجاء من له استفسار أو رأى أن يتكرم بعرضه هنا وشرح مطلبه تفصيلا وشكرا

هذه روابط ملفات PDF لهذه السلسة وهى من 3 أجزاء سأوالى إن شاء الله رفعها تباعا

موقع 4shaed
الأساسيات (مقاومات - مكثفات و دوائرها حتى الثنائيات)

الترانزيستور وحتى المكبر التفاضلى

الدوائر المتكاملة

موقع Drop Box

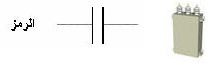
رابط الأساسيات

الترانزيستور وحتى المكبر التفاضلى على DropBox

الدوائر المتكاملة

إعجاب واحد (1)
2

بالتوفيق

3

شكرا اخى الكريم

4

بعد إكمال الرحلة السابقة المذكورة فى المقال الأول ابدأ بتقسيم فكرة الدائرة إلى مجموعة من الأجزاء المرتبطة ، كل جزء له وظيفة محددة
ابدأ بمزيد من التقسيم إن احتاج الأمر
ابدأ بتقسيم كل جزء إلى الوحدات السابق شرحها فى المقال الأول (مراحل) مثلا دائرة مكبر و دائرة توحيد ودائرة مقارنة الخ
راجع مسار الإشارة و الأوامر – أيضا تغذية التيار لكل الأجزاء (المراحل) .
استخدم لوحة تجميع Bread Board كما بالصورة

وهى ببساطة شكلها الخارجى على اليسار و التوصيل الداخلى لهذه الثقوب على اليمين. 4 خطوط تغذية بطول اللوحة ملونة باللونين الأزرق والأحمر لسهولة تمييز الجهود التى ستخصص لكل خط و مجموعة من الوصلات العرضية كل منها 5 ثقوب متجاورة. الفاصل فى المنتصف بعرض المتكاملة القياسية. يستخدم السلك المسمط المستخدم لمد كابلات الهاتف أو الشبكات لتوصيل الأطراف.
هذا موقع مفيد عن كيفية استخدامها


http://www.kpsec.freeuk.com/breadb.htm

قم بتجميع الدائرة مرحلة كل مرة ثم اختبر أدائها ،لا داعى لأن تجمع مراحل متعددة ثم تحتار أين العطل ، قم بتعديل قيم المكونات حسب الحاجة – إن احتاج الأمر.
لا تخف فمعظم الحالات المعقدة يمكن تبسيطها وغالبا يعود تحليلها لقانون أوم (فولت = تيار × معاوقة)
إذا كانت الدائرة اكبر من حجم اللوحة ارفع المراحل التى تمت و نجحت و ضع الوحدات التالية

أرجو أن تجعل دوائرك متقدمة وليست معقدة
الدائرة المتقدمة هى التى تستخدم أقل المكونات لأداء وظائف أكثر وتكون المكونات من احدث الطرز لا المنتهى إنتاجها فتكون رغم الأداء المتقدم سهلة الفهم للغير و سهلة الصيانة.
الدائرة المعقدة هى التى تستخدم الكثير من المكونات و العديد من التوصيلات المتراكبة والمتداخلة لتحقيق وظائف أقل فتكون أصعب فهما وأصعب فى الصيانة ويقضى الآخرون أوقات طويلة يقولون لماذا فعل هذا؟

مثال - دوائر التليفزيون :
كلنا نعلم أن التليفزيون يتكون من منتخب قنوات – تردد بينى – كاشف صورة – محدد النظام - فاصل ألوان مكبر بينى للصوت – كاشف صوت مكبرات للصوت والصورة دوائر تزامن أفقى و رأسى مولدات التردد الأفقى والرأسى

معظم الأنظمة اليابانية والأمريكية تتكون من مراحل بسيطة ومتعاقبة ، هذا لا يعنى أنها ليست متقدمة بالعكس فكل مرحلة تقوم بأدائها أفضل من الأجيال السابقة و تستخدم أحدث التقنية وتعطى أفضل النتائج. عند حدوث عطل تجد الباقى مازال يعمل فيكون لكل عطل - ظاهرة محددة - وهذا فى حد ذاته جزء من الصيانة (الإصلاح)
معظم الأنظمة الأوروبية تتكون من نفس المراحل بصورة معقدة أى ليس من السهل أن تضع حدودا - هذه مرحلة كذا - ومليئة بالوصلات المتراكبة (المتشعبة لأجزاء أخرى) التى ليس من السهل أن تعرف مغزاها أو هدفها وعند حدوث عطل فالظاهرة واحدة - جهاز قتيل - ولا تكاد تعرف إن كان الجهاز به عطل أم أن التيار مقطوع

برامج التمثيل أو تحليل الدوائر SPICE وسيلة جيدة لتقييم دوائرك قبل التنفيذ لكن يجب أن تعرف إمكانياتها جيدا فبعضها لا يؤدى دوره عند حدود معينة وقد يؤدى دورا أكثر كفاءة من الواقع فترى الدائرة تعمل على الحاسب وتفشل فى الواقع أو العكس - تذكر أنها وسائل تمثيلية أى تعتمد على بعض البيانات المعبرة عن سلوك الشيء المراد تمثيله ولن تكون كاملة ولن تكون هى الشيء نفسه.
مثلا الدائرة الشهيرة 555 ليس لها ملف بيانات SPICE كملف ترانزيستور مثلا أو مكبر عمليات ، لذلك تمثل بموديول عبارة عن مجموعة من المقارنات ومجزئ جهد الخ، لذا فهو تقريبى و أحيانا لا يأخذ معاملات تأخير الجهد داخل الدائرة فى الحسبان
لا تنظر بمنظار اسود ولكن الكمال لله وحدة لذلك لا تتوقع الكمال من الدوائر وبرامج الحاسب الخ ، اعرف أداتك وأدائها واستخدمها حيث تكون الأفضل ولكن عقلك – عقلك - عقلك هو من خلق الله وهو أكمل من الحاسب ، فهو يرى الدائرة كاملة من مدخلها لمخرجها بينما الحاسب الفائق القدرة يرى فقط قطعة واحدة فى المرة الواحدة.
استنتج وادرس وجرب فلا علم بدون تجارب ولا تجارب بدون خسارة والفشل دليل العمل والعمل طريق النجاح ولا تيأس فكل ميسر لما خلق له
من المرة القادمة إن شاء الله سنبدأ فى شرح المكونات

5

المقاومات:

لكى تصمم دائرة ما يجب أن تعرف أدواتك وقد قابلت طلبة يبحثون عن مقاومات 14.753 أوم .هكذا كانت نتيجة المعادلة وطبعا هذه القيمة لا تصنع كما أن هناك علاقة بين الدقة والقيمة أى أن هذه القيمة يجب أن تكون بدقة أوم لكل عشرة آلاف – أى 0.01% ، لذلك رأيت أن أبدأ بالمقاومات والمكثفات من الزاوية التى لا تدرس عادة فى الجامعات – لن نذكر قانون أوم إلا لاحقا ولكن ما تجده وما لا تبحث عنه فى السوق

المقاومات

المقاومة هى جسم يحتوى مادة مقاومة للتيار الكهربى ، لها طرفين على الأقل وقد يكون لها حتى 16 طرف.
حسب المادة المصنوع منها المقاومة يختلف أداؤها واستخدامها.
تعرف المقاومة بقيمتها ، القدرة بالوات ، الدقة % ، النوع أو خامة التصنيع ، الشكل وسنتناول كل صفة على حده
الشكل : هناك عدة أشكال
2طرف : كل المقاومات ذات القيمة الثابتة يكون لها طرفين ، إما سلكين أو أطراف لحام مباشرة على البورده أو عروتين لحام وفى القدرات الكبيرة مسامير رباط .
بعض المقاومات تحتوى فيوز بداخلها أو معها.
المقاومات ذات القدرات اكبر من 3 وات تتغير فى شكلها حيث توضع داخل واقى خزفى أو تلف عليه من الخارج كما تزود المقاومات 25وات أو أكثر أحيانا بمبرد برونزى معدنى.

المقاومات ذات 3طرف عادة تكون مقاومة متغيرة أو مجزئ جهد والطرف الثالث هو المنزلق ( المتغير ) ومنها 4 طرف حيث يكون الطرف الرابع يمثل نسبة ثابتة عليه بالإضافة للمتغير
يجب أن نذكر هنا أن المقاومات المتغيرة أيضا أنواع - نوعين حسب الشكل
أحدهما للتثبيت باللحام فى البورده و غالبا يسمى POT وهو للضبط
الآخر للواجهة لإعطاء المستخدم إمكانية التعديل حسب الرغبة كمفاتيح مستوى الصوت فى المكبرات و غيرها
النوع الثانى منه نوعين حسب التغيير
نوع خطى حيث تتغير القيمة خطيا مع زاوية دوران عمود المقبض و نوع لوغاريتمى حيث العلاقة لوغاريتمية بين الزاوية والقيمة وهو مصنوع لأن الأذن البشرية تشعر بارتفاع الصوت بمنحنى لوغاريتمى أى لو تضاعفت شدة الاهتزازات الصوتية لن تشعر بارتفاعه للضعف وهذا هو السبب فى استخدام وحدات الديسيبل لقياس المكبرات

أيضا هناك ما يحتاج للدوران 10 دورات وتستخدم للضبط الدقيق

منها تثبيت بوردة للضبط الدقيق و منها تثبيت واجهة للاختيار الدقيق حيث تجدها فى أجهزة القياس مثل الأوسيلوسكوب و مولدات التردد.
و كيف نعرف أين هو من هذه الدورات؟
صنعت مقابض خاصة للتركيب عليها تحتوى “ساعة” أو تدريج من 1:100 على الواجهة و كل دورة كاملة تحرك أرقام داخل نافذة إما بالزيادة أو النقصان من 0 إلى 9 لتحديد أى دورة، و هكذا يمكنك تقدير بنسبة 1:1000 من قيمتها خاصة و أن بعضها تصل دقته إلى +/- 0.5%. أيضا تزود بذراع لتثبيت المقبض حتى لا يتحرك عفويا لأى سبب
ولماذا توضع أرقام على أطرافه؟!! هل هناك فرق؟
نعم ، عند الدوران عكس عقارب الساعة، تحرك المنزلق نحو الطرف 1 والعكس بالعكس وهذا ليمكن المستخدم من التوصيل بصورة تجعل الدوران مع الساعة يتوافق مع زيادة الظاهرة – و أؤكد الظاهرة وليس الفولت.
ما معنى هذا؟
ببساطة لو زيادة الفولت تسبب تقليل إضاءة شاشة ما وجب عكس الأطراف لأن المستخدم يتوقع الدوران يمين لزيادة الضوء.
هذا الرابط به معلومات كثيرة أيضا عن المقاومات


و هذا عن المقاومات المتغيرة

الأطراف الأكثر تكون مجموعة من المقاومات Resistor Pack داخل جسم واحد بعضها تحتوى 4 أو 6 أو 8 مقاومات لها طرف مشترك وشكلها كالمشط وبعضها مجرد مجموعة غير متصلة تشبه الدائرة المتكاملة IC وتكون المقاومات متجاورة
القدرة
تكون بالقيم 1/8 ،1/4 ،1/2 ،1،2 ،3 ،5 ،7 ،10 ،15 الخ وذلك للمقاومات ذات أسلاك التوصيل
المقاومات الأصغر للحام بدون أطراف وعلى السطح Surface Mount فتبدأ من 1/16 إلى 1 وات
الدقة :
فى السابق كانت تصنع بدقة 20% ولكن الآن مع تقدم التقنية ، حتى مقاومات 10% أصبحت نادرة الوجود وأغلبها 5%
توجد مقاومات بدقة2% و 1% ولكنها أقل تواجدا واعلى سعرا و يمكنك طلب 0.5% أو أفضل
يجب أن نفهم معنى الدقة – لو لدى مقاومة 10 كيلو بدقة 5% فهذا يعنى أن قيمتها الحقيقة قد تكون بين 10500 أوم إلى 9500 أوم – لهذا يجب أن تقرب نتائج الحسابات لأقرب قيمة عملية ممكن تواجدها أو اختيار دقة أعلى إن دعت الضرورة
القيمة
توجد المقاومات بقيم قياسية على أساس دقة 10% ولا نتوقع أن نجد ما نريد ولكن يمكنك تجميع القيم الوسطى . هذه القيم ستذكر من 10 إلى 99 أما الباقى مضاعفات هذه القيم ×10 أو 10÷ وهكذا
10- 11- 12- 13- 14- 15- 16.5- 18- 20- 22- 24- 27- 30- 33- 36- 39- 43- 47- 51- 56- 61- 68- 75- 82- 91
بقى أن نتكلم عن مادة التصنيع
هناك مقاومات ذات معامل حرارى سلبى أى تتناقص بارتفاع درجة الحرارة (أساسها كربونى) وأخرى ذات معامل حرارى موجب أى تتزايد بارتفاع درجة الحرارة (أساسها معدنى) وتحاول الدراسات أن تقلل هذه المعاملات لقيم لا تذكر كما أن بعضها يصنع خصيصا لإظهار هذه الخاصية وجعلها أكثر انتظاما لاستخدامها كحساسات للحرارة مثل BT100 وهى ذات معامل حرارى موجب وهناك أنواع ذات معامل حرارى سالب تصنع من أشباه الموصلات.
المقاومات الكربونية:
وتصنع من مركب كربونى بشكل أسطوانى وهى تناسب القيم الكبيرة وهى أيضا مصدر للضوضاء والشوشرة لذلك لا تناسب مراحل التكبير الأولية Pre-Amplifiers
مقاومات الفيلم الكربونى
تصنع بطلاء قالب سيراميك بمخلوط كربونى وبعد الجفاف يمكن نحت مسار لولبى للحصول على القيم الأعلى ، نفس المحاسن والعيوب كالسابق
مقاومات الفيلم المعدنى
وتصنع بتبخير وتكثيف المعدن المطلوب على القالب السيراميك وهى أفضلهم من ناحية الخواص واقل ضوضاء لذلك تستخدم فى مراحل التكبير الأولية Pre-Amplifiers
مقاومات السلك الملفوف
ذات دقة عالية وضوضاء قليلة وقدرات (وات) كبيرة ولكن يعيبها أنها لا تناسب الترددات المرتفعة لتشابه شكلها مع الملفات فهى تتصرف كملف عند بعض الترددات ثم يحدث لها رنين عند زيادة التردد ثم تنقلب لمكثف عند الترددات الأعلى تماما كدائرة رنين التوازى وعند الشراء يذكر هذا التردد Self Resonating frequency فى الخواص
مقاومات الفيلم الكربونى تعانى بشكل أقل من هذه الظاهرة وأفضلهم مقاومات الفيلم المعدنى
فى حالة الدوائر التى تتحاشى هذه الخواص كدوائر التردد العالى جدا ، ينص صراحة على مقاومات خالية الحث non inductive resistor وهى تصنع خصيصا بهذه الصفة
هذا الموقع به معلومات كثيرة عن المقاومات
هناك مقاومات تتغير مع شدة الإضاءة و تستخدم كحساسات للإضاءة


مقاومات تعتمد على الجهد فتقل قيمتها عند ارتفاع الجهد عن قيمة محددة و تستخدم فى التخلص من التداخلات التى تحدث على خطوط التغذية

المرة القادمة إن شاء الله سنتحدث عن المكثفات

6

المكثفات:
تنقسم المكثفات لقسمين رئيسيين هما مكثفات التطبيقات الصناعية و مكثفات الدوائر الإلكترونية

مكثفات التطبيقات الصناعية
**وهى المستخدمة مع الآلات والموتورات كبادئ إدارة أو مساعد بدء تشغيل للموتورات وتحسين معامل القدرة للمكونات كمصابيح الفلوريسنت أو للموقع ككل وتكون عادة بقيم 1 ميكروفاراد فأكبر. **
تشترك هذه المكثفات بأنها تتعرض لجهود مترددة عالية 220 أو اعلى وتصل إلى أكثر من ألف فولت أحيانا كثيرة و أيضا يمر فيها تيار كبير بدء من 0.01 أمبير إلى بضع مئات فى حالات تحسين معامل القدرة ويراعى فى تصميمها تشتيت الحرارة التى قد تتولد نتيجة ظروف التشغيل.

لذلك تكون كلها عديمة القطبية ، تتحمل جهود عالية ، صلبة ميكانيكيا ، ذات كفاءة عالية لتقليل الحرارة الناتجة، جيدة التهوية ومعدلات نقل الحرارة من الداخل للخارج عالية حتى لا تصل لدرجات حرارة تتلف معها أثناء التشغيل – الحجم أو الوزن - لا يهم

مثلا لتحسين معامل القدرة لمصباح الفلوريسنت العادى تستخدم مكثف 2 إلى 4 مايكرو
أما لتحسين معامل القدرة Power Factor لموقع ما كمصنع أو ما شابه فلا يوجد مكثف يتحمل هذا القدر من التيار الذى قد يصل عدة مئات من الأمبير ، لذلك تستخدم بعض أنواع الموتورات التى عندما تعمل بدون حمل تظهر كحمل سعوى (مكثف) على الخط ، فباختيار طاقة الموتور المناسبة للأمبير المتوقع ثم تعديل الحمل (عادة يكون بمثابة فرملة على الموتور) يمكن ضبط قيمة السعة المطلوبة

**قديما كانت تصنع المادة العازلة من ورق مشرب بالزيت وكانت تسمى مكثفات ورقية أما الآن فهناك عدة أنواع أفضل. **
فى هذا الرابط معلومات أخرى عن المكثفات الصناعية
http://www.abb.com/product/us/9AAC710017.aspx

لا تستخدم المكثفات المخصصة للدوائر الإلكترونية فى التطبيقات الصناعية فغالبا ما تسخن و تتلف بسبب ارتفاع درجة الحرارة.

مكثفات الدوائر الإلكترونية

تتباين مكثفات الدوائر الإلكترونية فى خواصها وقيمها إذ تتراوح ما بين 3 بيكو فاراد أو أقل إلى عدة فاراد حسب الاستخدام وكذا الجهد من 3 فولت إلى عدة آلاف والحجم من أقل من ملليمتر واحد لحجم اكبر من قبضة اليد و يحتاج حزام معدنى ومسامير للتثبيت

تعرف المكثفات بقيمتها ، الجهد بالفولت ، الدقة % ، أقصى تردد أو الرنين الحر، النوع أو خامة التصنيع ، درجة الحرارة ، الشكل

القيمة
تبنى قيم المكثفات على أساس 20% فتجد القيم التالية ومضاعفاتها
**10 ، 12 ، 15 ،18 ، 22 ، 27 ، 33 ، ،39 ، 47 ، 56 ، 68 ، 82 ، 100 **

أما المكثفات المتغيرة فتكون
مكثفات الضبط الدقيق إما بقيمة ضبط من 4 إلى 40 بيكو فاراد أو من 10 إلى 70 بيكو فاراد
مكثفات التنغيم (اختيار القنوات) عادة أكثر من واحد على محور ميكانيكى واحد و إن لم يكن ذلك واضحا بالشكل لكن عدد الأطراف يكشف ذلك، الشكل يبين الطرف العلوى المستخدم فى اختيار المحطات بينما السطح السفلى يحتوى مكثف ضبط دقيق لكل واحد من هذه المكثفات لضبط قيمة البدء.

** تكون هذه المكثفات بقيمة ضبط من 10 إلى 360 بيكو فاراد مهما اختلف الحجم والشكل و نطاق المحطات المستخدم فيه وهو يحتوى على مكثفين على الأقل أحدهما لدائرة الهوائى والآخر للمذبذب المحلى.**
مكثفات التنغيم الإلكترونية وهى ثنائى من أشباه الموصلات يوصل عكسيا للعمل كمكثف متغير من 4 إلى 70 بيكو فاراد حسب الجهد العكسى الواقع عليه و سيأتى ذكره فيما بعد.

الجهد بالفولت
للجهد الذى تتحمله المكثفات قيم محددة وهى غالبا
3.3 فولت ، 6.3 ، 12 ، 16 ، 25 ، 35 ، 50 ، 100 ، 200 ، 400 ، 600 ، 800 ، 1000 ، 1200 ، 1500 ، 2000 ، 3000 ، 4000 ، 6000 فولت
ونظرا لاختلاف المعايير الأوروبية واليابانية والأمريكية فقد تجد أحيانا قيم متوسطة ، يمكن عادة استخدام الجهد الأعلى مباشرة
الجهد السابق ذكره هو جهد مستمر فقط ما لم يذكر صراحة غير ذلك ويميز بعلامة =
**المكثفات التى تستخدم مع التيار المتردد يذكر عليها صراحة قيمة الجهد المتردد . **
تذكر قيمة أخرى للجهد المتردد (إما على جسم المكثف أو فى صفحة البيانات الخاصة بهذا النوع) وهى تعنى أعلى جهد متردد يمكن تواجده منفردا أو مجتمعا مع الجهد المستمر – والسبب طبعا أنه يسبب ارتفاع درجة الحرارة والتى بدورها تؤثر على جودة المكثف و ربما يتلف
إذا كان المكثف من النوع ذى القطبية – لا تعرضه لقطبية معكوسة تحت أى ظرف
لماذا والمكثف به عازل ولا يمرر تيار، المفترض أن المكثف لا يتأثر إن كان الجهد مستمر أم متردد؟
حقا لكن هناك سببين
أولهما أن العازل ليس مثاليا وهناك تيار تسريب يقل كلما كان العازل أفضل
**والثانى أن الإلكترونات تدور حول النواة. الجهد الكهربى يسبب أن المسار يأخذ الشكل البيضاوى كما بالرسم التالى والذى يتجه نحو القطب الموجب. **
تغير هذا الانحراف يسبب مرور تيار متردد كنتيجة لحركة هذه الإلكترونات حول النواة مسببا ارتفاع فى درجة حرارة العازل و ينتهى بتلفه
** **

الدقة %
**الدقة يعتمد معناها على نوع المكثف **
كل المكثفات الغير كيماوية تكون الدقة هى + / - نفس القيمة مثلا + / - 10%
كل المكثفات الكيماوية تكون الدقة هى الحد الأدنى أما الحد الأعلى فقد يختلف كثيرا بين الأنواع فمثلا مكثف 20% يعنى أنه لن يقل عن 20% من القيمة المدونة ولكن قد يكون أعلى 20 % أو أكثر وذلك لأنها تتغير خواصها بالاستخدام كما سيلى ،لذا فالمكثفات الكيماوية لا تصلح للتوقيت (Timer) و المرشحات الدقيقة و دوائر الرنين لكنها تناسب مثلا المرشحات التى تزيل كل المركبة المترددة من وحدة التغذية مثلا (By Pass) حيث كلما زادت القيمة كان ذلك أفضل

أقصى تردد أو الرنين الحر
المكثفات تصنع من شريطين من المعدن (الألمونيوم غالبا) وبينهما شريط عازل ثم تلف مجموعة الشرائط حول نفسها مما يجعلها تشبه الملف ، من هنا يتكون ما يشبه دائرة رنين ذاتية تجعل له رنين حر ، بعد هذا التردد يصبح المكثف فعليا ملف ذو حث معلوم ، لذا لا يمكن استخدام هذا المكثف قرب هذا التردد و يجب اللجوء لنوع غيره
**شكل وأبعاد المكثف هى العوامل الرئيسية فى تحديد هذا التردد لذا المكثفات التى تصنع من شرائح مسطحة تناسب الترددات الأعلى مثل مكثفات الميكا. **

النوع أو خامة التصنيع
**قليلا ما يؤثر المعدن فى خواص المكثف ولكن المادة العازلة لها التأثير الأكبر ، تنقسم إلى نوعين رئيسيين المكثفات الكيماوية و المكثفات غير الكيماوية **

المكثفات الكيماوية
النوع الالكتروليتى :تحتوى محلول كيماوى يرسب أكسيد الألمونيوم كمادة عازلة وهو يتكون نتيجة الجهد الواقع عليه ، ولذلك عند عدم استخدامه لفترة قد تتآكل هذه الطبقة وتسبب تغيرا فى قيمته ولكنها تعود عند الاستخدام
هذا النوع يستخدم كمرشح لإمكانية الحصول على قيم كبيرة تصل لقرابة فاراد ولكن لا يصلح للزمن أو التوقيت أو ضبط التردد لعدم ثبات قيمته وكونه وحيد القطبية أى أن عكس الجهد عليه يجعله موصل للتيار و يحدث قصر وسخونة ثم انفجار ، ومعظم دوائر التوقيت تعرض المكثفات لعكس القطبية.
لا تصلح للترددات أعلى من عدة كيلو ذ/ث لكونه شريط طويل ملفوف من الألمونيوم
هناك خاصية أخرى يجب الحذر منها لهذا النوع من المكثفات هى خاصية البطارية - لاحظ مما سبق أن العازل مادة كيمائية تتكون بوضع الجهد عليه ، فمن الطبيعى أن عند رفع الجهد – تبدأ هذه المادة فى التحلل مولدة جهدا كهربيا قليلا قد يصل لفولت أو أكثر ، هذا الجهد – رغم أنه لا يكفى لتوليد تيار محسوس – إلا أنه قادر على التأثير على دوائر التوقيت و المقارنة وخلافه وللأسف لا يمكن التنبؤ بها فهى تظهر فى واحد أكثر من غيره .

لذا يستخدم فى وحدات التغذية لترشيح مركبات التيار العمومى 50-60 ذ/ث و يعتمد على أنواع أخرى لترشيح مكونات الترددات الأعلى التى تتواجد على خطوط التغذية والتى تتولد من أداء الدوائر المختلفة.

نوع تانتالوم : يحتوى أكسيد التانتالوم بدلا من الألمونيوم وهو لا يحتوى محلول لذلك يسمى Solid Tantalum وهو انسب للترددات الأعلى التى تصل إلى 1 مليون ذ/ث.
لاحظ هنا أن ما يناسب التردد العالى لا يناسب التردد المنخفض والعكس بالعكس ، لهذا عند تصميم دوائر ذات تردد عالى لا بد من جمع هذه المكثفات معا مثلا 0.1 سيراميك مع آخر 100 ميكرو فلا تظن أن الأكبر قيمة يغنى عن الأصغر قيمة فكل منها يعمل عند تردد حيث يفشل الآخر.
القواعد التى اتفق عليها أن كل كارت يجب أن يحتوى على الأقل 100ميكرو عند دخول خطوط التغذية إليه لترشيح مركبات التيار العمومى – بصرف النظر عن الكارت الأم و ما يحتوى من مكثفات – ثم بعد ذلك أضف المكثفات الصغيرة حيث توجد دوائر تذبذب أو مكبرات تيار أو وحدات رقمية.

المكثفات غير الكيماوية موضوع الحلقة القادمة إن شاء الله

7

المكثفات غير الكيماوية

تتميز بعدم القطبية وثبات القيمة و إمكانية الحصول على دقة عالية ، لذلك يستخدم فى التوقيت و ضبط التردد
القيم و المواصفات كما فى البند السابق

أشهر الأنواع هى
بوليستر : تستخدم مادة البوليستر كعازل يعطى إمكانية الحصول على جهد أعلى ، سهولة التوافر ، رخص التكلفة ، مستقر مع تغير درجة الحرارة نسبة الدقة من 5 إلى 10 %
بولى بروبيلين : أدق من السابق حيث يمكن أن يصل إلى 1% وانسب للترددات الأعلى
بوليستيرين : لا يناسب الترددات العالية لكونه ملفوف – يناسب المرشحات والتوقيت
بوليستيرين ذو فيلم المعدنى : معروف باسم مايلار والاختلاف أن المعدن يكون فيلم رقيق على العازل مما يجعل له خواص فريدة منها عند حدوث قصر بداخله فالشرارة تأكل المعدن والعازل تاركة المكثف أقل قليلا فى قيمته دون حدوث قصر لعدم تكون كربون من الاحتراق وعدم توافر معدن بغزارة تؤدى لالتحام الطبقات مكونا قصر مستديم
ذات جودة عالية ، عالى الثبات ، يتحمل الحرارة ، جيد بصورة عامة
إيبوكسى : يمكن الحصول على قيم كبيرة ولكن لا يناسب الترددات العالية
سيراميك : وهى انسب الأنواع كمرشحات التردد العالى ، تتأثر بالحرارة لذلك لا تستخدم فى الرنين لتحديد التردد وتصنع بعدة أشكال و توجد فى كل الدوائر المنطقية لتنقية خطوط التغذية وتوزع على البوردة تقريبا بجوار كل 1-3 دائرة متكاملة IC

سيراميك متعدد الطبقات : مناسب للترددات المرتفعة و أكثر ثباتا ولكن لا يناسب الترددات العالية جدا 10 ميجا فأكثر ، ويستخدم لترشيح الترددات وليس فى توليدها
ميكا – فضة :انسب الأنواع للترددات العالية كدوائر رنين الخ عالى الثبات ، اعلى سعرا ولكنه يساوى التكلفة

درجة الحرارة
هو المدى الذى يمكن للمكثف أن يعمل فيه دون أن تتغير خواصه أو يتعرض للتلف من قيم تحت الصفر المئوى إلى +35 أو +45 … حتى + 125
جدير بالذكر أنها ليست فقط درجة حرارة الوسط المحيط فقط ولكنها تشمل الحرارة المتولدة داخله و أيضا تظل قيمته فى حدود الدقة المحددة
عندما يتعرض المكثف للجهد المتردد فإن إلكترونات المادة العازلة تغير مدارها حول النواة من مدار دائرى لمدار بيضاوى يتابع القيم اللحظية للجهد متسببة فى مرور تيار تسريب صغير Leakage Current لكنه مؤثر فى ارتفاع درجة حرارة المكثف الداخلية وهذا ما يؤثر فى أداؤه لذلك هناك بعض المكثفات تفشل عند تعرضها لهذه الظروف و تلاحظ بان تعمل عند البدء وبعد فترة قصيرة تتغير النتائج نتيجة لتغير قيمة المكثف.

الشكل
الشكل كما سيق الذكر له تأثير مباشر على التردد وأيضا إمكانية أن يحل مكثف محل آخر إذ بعضها أطرافه من جهة واحدة وأخرى من جهتين - المكثفات الأكبر حجما تكون أكثر عرضة للتداخلات وتأثير المراحل على بعضها من المكثفات الصغيرة فمثلا المكثفات التى يستخدم فى الدوائر ذات التثبيت السطحى Surface Mount لا يناسبها أحيانا الاستبدال بأخرى اكبر حجما

فيما يلى بعض المواقع التى تقدم معلومات إضافية عن المكثفات
http://www.radio-electronics.com/inf...itor_types.php
http://www.uoguelph.ca/~antoon/gadgets/caps/caps.html

تكلمنا كثيرا عن المكثفات – ما هى قيمة المكثف
حسنا – المكثف سعة مثل حوض يحتوى سعة إذن كم يكون “واسعا” هذا الشىء
لو وضعنا به أشياء و لم ترتفع كثيرا إذا هو واسع و إن ارتفعت إذن هو ضيق
أى سعته يعبر عنها بقسمة كميه الأشياء على ارتفاعها
و كهربيا كمية الكهرباء التى دخلت فى وحدة زمن مقسوما على ارتفاع الجهد على طرفيه
كميه الكهرباء ؟ هل هذه مزحة؟
كلا لو تذكرنا كم إلكترون فى الكولوم والأمبير هو واحد كولوم فى الثانية لأمكننا أن نقول
السعة = مقدار الشحنة الداخلة ÷ الجهد المرتفع فى وحدة الزمن = مقدار الشحنة ÷ فرق الجهد
C = Q \ ∆V
C= I*T\∆V
أى السعة = التيار × الزمن ÷ الفولت الذى تغير أو المسمى فرق الجهد ( ∆V)

لو نذكر هذه العلاقة عندما نتحدث عن الزمن و دوائر التزامن.

الملفات موضوع الحلقة القادمة و ما هى العوامل المؤثرة خلاف الحث عند اختيار ملف.

8

الملفات

تنقسم إلى ملفات قدرة عالية وملفات للدوائر الإلكترونية
ملفات القدرة العالية أو الصناعية
تكون عادة لفات من سلك نحاسى معزول مناسب القطر على قلب من شرائح الحديد السليكون كالمحولات ولكن تختلف عنها فى وجود فجوة لمنع تشبع الحديد حتى لا يفقد قيمة الحث – العزل أحيانا بالورنيش فقط أو طبقة من الورنيش و طبقة من خيوط عازلة

أحيانا توصل مع الموتورات أو مع المحولات التى تحول حمل معين من 3 فاز إلى مصدر تيار فاز واحد وغالبا مع وحدات توحيد التيار المتردد باستخدام الثايريستور .
يمكنك التفريق بين المحول والملف بسهولة بالنظر إلى جانب الحديد الذى يتكون من مقطعى E , I ففى المحولات تتبادل المقاطع حتى لا تتكون فجوة أما فى الملف فيكون كل مقطع مجمع على حدة ثم يوضع الملف فى بكرة توضع حول الجزء الأوسط من حرف E ثم توضع المجموعة الأخرى وتوضع بينهما غالبا قطعة من الفيبر سمكها يحدد عرض الفجوة وتربط بشنبر (حزام معدنى) يمسك القطع معا، كما أن غالبا يكون الملف ذو طرفين أما المحول فعلى الأقل ثلاثة أطراف.
يحدد الملف هنا بقيمة الحث بالهنرى و أقصى تيار مستمر يمكن أن يحتمله الملف و أيضا أقصى تيار يتحمله السلك (متردد + مستمر). وجدير بالذكر أن أقصى تيار مستمر يذكر حين يخشى أن يسبب هذا التيار تشبع الحديد فتقل قيمة الحث كثيرا . ونظرا لأن هذا التشبع لا يحدث دوما ولكن فقط عند قمم التيار المتردد حين يضاف المجال الناشئ من نصف الذبذبة مع المجال الناشئ من التيار المستمر مسببا تشبع ، فيحدث ذلك تشويها فى شكل الموجة مسببا توليد توافقيات وحدوث زن فى الملف.
جدير بالذكر أن الدقة هنا ليست ذات أهمية لأن الاستخدام غالبا تصحيح معامل قدرة أو التخلص من ضوضاء ما.

ملفات الدوائر الإلكترونية

تستخدم الملفات عادة فى أحد تطبيقات ثلاث
دوائر رنين - ملف خانق - ملف حمل ورغم اختلاف المسميات إلا أن الهدف واحد هو اختيار تردد أو مجموعة ترددات إما للمرور أو للمنع أما ملف الحمل يستخدم لتغيير طبيعة الحمل من حمل سعوى إلى حثى لأن كل أشباه الموصلات مثل الترانزيستور مثلا لا تتقبل الأحمال السعويه و لكن تقبل الأحمال الحثية

تعرف الملفات بقيمتها ، الدقة % ، النوع أو خامة التصنيع ، مقاومة التوالى أو معامل الجودة ، التيار بالأمبير ، الرنين الحر ، الشكل

القيمة
هى قيمة الملف بالهنرى ، مللى هنرى أو نانو هنرى أو ميكرو هنرى وتعتمد أساسا على أبعاد الملف وعدد لفاته ونصف فطر اللفات ومادة القلب
القيم نفسها الموجودة للمكثفات موجودة أيضا للملفات أى على أساس 20%

الدقة
غالبا توجد 10% ، 5% و أحيانا قليلة 2% أو 1%

النوع أو خامة التصنيع
يقصد بها نوع القلب والذى يحدد لحد بعيد نطاق الترددات المناسب للملف
القلب الهوائى حيث يلف الملف على مشكل من الفيبر أو البلاستيك ويترك قلبه خاليا ، يناسب كافة الترددات لكن قيمته تكون صغيرة لصعوبة التشكيل ، كثرة اللفات تزيد من السعة المتولدة بين اللفات وبعضها ، مسببة الرنين عند ترددات منخفضة
هذا النوع حساس للسعة الشاردة والالتقاط من المجالات القريبة كما أن وضعه داخل علبة معدنية بهدف الحجب المغناطيسى أو الكهربى يزيد من السعة الشاردة و يغير التردد.
القلب الحديدى وتصنع من قلب من رقائق حديد السليكون المعزول مما يسبب ارتفاع الحث بنسبة كبيرة ، التيارات الدوامية فى الحديد تسبب فقدا عاليا عند ترددات حوالى 1000 ذ/ث فما فوق لذلك يناسب الترددات المنخفضة فقط
قلب برادة الحديد تمزج برادة الحديد بمادة عازلة ولاصقة كالسيراميك أو الإيبوكسى لتقليل التيارات الدوامية ويناسب هذا النوع ترددات أعلى حتى عدة ميجا هيرتز حسب مواصفات المادة.
قلب فرايت ويصنع من خامات أو مركبات حديدية لها مواصفات متنوعة تناسب ترددات من فوق سمعية لبعض أنواع تستخدم فى دوائر الميكرو ويف

مقاومة التوالى أو معامل الجودة
السلك المصنوع منه الملف له مقاومة أومية ، هذه المقاومة – مهما صغرت - تسبب فقدا فى التيار ومن ثم تقلل جودة الملف ويتسع نطاق الترددات التى تمر من دائرة الرنين المصنوع منها هذا الملف
Q=ωL\r
حيث Q هى معامل الجودة
× 2 = ω ط × التردد
= L الحث بالهنرى ، r مقاومة السلك بالأوم
BW= fo \ Q
حيث BW هو نطاق الترددات
، fo هو تردد الرنين

التيار بالأمبير
هو أقصى تيار مستمر يمكنه المرور نتيجة قطر السلك المستخدم والذى قد يكون 0.1 مم أو أقل وأيضا حتى لا يحدث تشبع لمادة القلب
هذه الخاصية هامة جدا إذا كان الملف سيوصل بين ترانزيستور و مصدر التيار مباشرة كما فى دوائر الذبذبات ، لم تسمع عنها من قبل أليس كذلك؟ - عفوا عندما يقال استخدم ملف رقم كذا من شركة كذا أو سلك قطره كذا و لف …الخ قد حددت كل هذه العوامل سويا

الرنين الحر
هو نتيجة الحث الناتج من اللفات والقلب مع السعة الناتجة من تجاور اللفات مشكلا دائرة رنين توازى تجعل الملف له رنين عند تردد معين و بعده قد يكون له قيمة سعويه بدلا من حث

الشكل
يحدد ملائمة الملف لاستخدام معين كالأطراف و أنواعها أو كونه مكعب صغير لدوائر التثبيت السطحى أو ملفوف على قلب دائرى أو غيرة كمرشحات لخطوط التغذية .

الرابط التالى به مزيد من المعلومات


وفى الرابط التالى موقع لحساب الملفات ذات الطبقة الواحدة و المتعددة الطبقات
http://www.captain.at/electronics/coils/

كيف نقرأ قيم هذه المكونات؟ هذا موضوعنا القادم إن شاء الله

9

كيف نقرأ قيم المكونات؟
** هناك طريقتان لتسجيل قيم المكونات هما الكتابة و الألوان**
الكتابة تعتمد الأرقام والحروف حيث تدل الحروف على قيمة العدد كونه بالآحاد أم ألاف أم ملايين فمثلا
K,k تعنى ألف من كلمة كيلو
M تعنى مليون ولكن m تعنى مللى أى جزء من ألف ولنتذكر فالحرف الكبير للقيمة الكبيرة
U,u و الحرف اللاتينى “ميو”  تعنى مايكرو وهى جزء من مليون
N,n تعنى نانو وهى جزء من ألف مليون أى 10¯9
**و أخيرا P,p تعنى بيكو وهى جزء من مليون المليون أى 10 -12 **
**أما الأحرف R,F,H فهى تعنى الوحدة من المقاومة أو المكثف أو الملف بالترتيب فمثلا **
56R تعنى مقاومة 56 أوم لاحظ أن الرقم يسار الحرف بينما
0R2 و تكتب بدون صفر أحينا R2 على القطعة ذاتها (لا على الرسم) تعنى 0.2 أوم
3F3 تعنى مكثف 3.3 فاراد
20H تعنى ملف 20 هنرى
أيضا العلامة العشرية تكتب إما بالطريقة التقليدية فى وسط الرقم أو بوضع الحرف مكانها فمثلا
4K7 بجوار مقاومة تعنى 4.7 كيلو أوم و التى قد تكتب 4.7K أيضا
5n6 بجوار مكثف تعنى 5.6 نانو فاراد و التى قد تكتب 5.6nF أيضا
أيضا 4m7 بجوار ملف تعنى قيمته 4.7 مللى هنرى و التى قد تكتب 4.7mH أيضا.

هناك طريقة الأرقام الثلاث فمثلا تكتب 102 وهذه لا تعنى مائه و لكن هى تعنى ألف لأن الرقم الأيمن وهو هنا 2 يعنى عدد الأصفار على يمين الرقم أى نستبدل 2 بصفرين ليصبح الرقم 1000 و بالمثل 104 تعنى 100000 أى مائة ألف
حسنا هذا فى المقاومات مفهوم و ماذا عن الباقى!!
تعتبر وحدات المكثف البيكوفاراد حيث لا يوجد عمليا أصغر منها و تعتبر وحدة الملف الميكرو هنرى حيث لا يوجد أيضا عمليا أصغر منها

الطريقة الثانية بالألوان وهى موضوعنا القادم بإذن الله

10

تمييز المكونات بالألوان

الطريقة الأخيرة تستخدم الألوان لتحديد القيم حيث يوضع اللون الأول لتحديد الرقم الأول أى الأكبر ثم اللون الثانى لتحديد الرقم التالى ثم عدد الأصفار.
كيف تحدد الأرقام بالألوان؟ نحن نرى بالضوء لذا لماذا لا نتبناه؟؟
حسنا لنبدأ بالأسود وهو يعنى لا ضوء و يناسب الرقم صفر و الأبيض الذى يعنى كل الضوء لأعلى رقم وهو 9 و طبعا لا بأس من اعتبار الرمادى التالى للرقم 9 أى 8 فهو كل الطيف ولكن أقل فى الشدة
باقى الألوان يكون من السهل أن نتذكرها بتذكر “قوس قزح” أى ألوان الطيف حيث تبدأ بالأحمر أدناهم ثم البرتقالى ثم الأصفر ثم الأخضر ثم الأزرق فالبنفسجى
و من لديه خبرة بالرسم و الألوان سيجد أن البرتقالى هو التدرج الطبيعى من الأحمر للأصفر لأن مزج الأحمر والأصفر يعطى البرتقالى
نفس الأمر بين الأصفر والأزرق يأتى الأخضر
وبالمثل الأحمر مع الأزرق يأتى البنفسجى

وهكذا فلقراءة المقاومة المرسومة بالشكل، نبدأ من جهة اللون المجاور للحافة فنجد أحمر =2 ثم بنفسجى =7 ثم أصفر = 0000 و بهذا فالقيمة 270000 أى 270ك أوم
إذن لو كان اللون الثالث أسود فهذا يعنى أنه لا يوجد أصفار كما بالرسم الأسفل فتكون 27 أوم فقط.
كيف إذن نحصل على 2.7 أوم أو 0.27 أوم؟؟
حسنا لو كان الشريط الثالث ذهبيا نقسم على 10 أى 2.7 أوم ولو كان فضيا نقسم على 100 فتكون 0.27 أوم
هذه المقاومة تكون ذات دقة 20% لأن عدد الألوان هو ثلاث فقط، و لو تذكرنا ترتيب القيم فى شرح المقاومات سنتذكر لماذا ثلاث أرقام تكفى للتعبير عنها .
بوضع شريط عريض بعد الألوان السابقة فضى اللون يعنى أنها ذات دقة 10% ولو كان ذهبى اللون تكون 5% وعادة ما يكون هذا الشريط أعرض من الباقى.
ماذا نفعل عندما نريد دقة أعلى من 5% مثلا 2% أو 1%؟؟
لنأخذ مثال عددى فمقاومة 10ك مثلا بدقة 1% لن تتغير بأكثر من 100 أوم أى ستكون من 9900 الى10100 أو 9.9ك حتى 10.1 ك وهذا يتيح تصنيع مقاومة 10.5 ك ،10.7 ك الخ لذا يجب أن نضيف رقم ثالث للطريقة السابقة أى حزام ذو لون يعبر عن الرقم الثالث. فتكون مثلا مقاومة 12.3 ك هكذا

نلاحظ أن شريط الدقة الآن بنى اللون ليوضح أن الدقة 1% ولو كان أحمر اللون ستكون الدقة 2 %
بقى أن نذكر أن بعض المكونات الأخرى مثل الملفات و بعض المكثفات القديمة استخدمت أسلوب مشابه ولكن مبنى على أساس الجسم ثم الطرف و أخيرا النقطة هكذا

عند توصيل أى من المكونات السابقة لمصدر جهد فهى تتصرف حسب قانون أوم وهو موضوع الحلقة القادمة

11

قانون أوم

دائما نبدأ بالجهد = الخ - هل حقا نفهم كل كلمة منه؟
هل نعلم أن ليس هناك ما يسمى قانون أوم!!
**ملحوظة هامة جدا : **
أنا لا أقلل من شأن أى من الآتى ذكرهم فيكفيهم تقديرا أنهم لاحظوا ما لم يلاحظه غيرهم ولكن فقط أحاول تقليل الغموض حول الكهرباء والذى ينبت الخوف

هناك قانون واحد فى الحياة أن القوة المؤثرة كلما زادت استطاعت أن تحرك أشياء أكثر بداية من حركة كرسى فى المنزل أو ضغط صاحب نفوذ - إلى مسار الكواكب والنجوم و المجرات ، فقط لاحظه السيد/ نيوتن فى الأجسام فسمى قانون نيوتن
ق = ك × ج
ولاحظه باسكال فى السوائل بالضغط و معدل سريان السائل و معاوقة المسار ولاحظه أوم فى الكهرباء .
فالسيد أوم قال قانون نيوتن بطريقته و السيد نيوتن كذلك
لنرى كيف هذا
السيد نيوتن قال ق = ك × ج حيث ق القوة و حيث ج التسارع أو الجريان و حيث ك الكتلة – فإن كانت لشىء مثل البلى كانت عدد البلى مضروبا فى كم بلية تعبر فى الثانية و مثلها عدد الإلكترونات فى الثانية .
**وهذا قانون أوم حيث ق القوة “الدافعة الكهربية” ونسميها فولت ، الجريان هو معكوس معنى المقاومة و الكتلة هى كم إلكترون تعبر فى الثانية و قد تم تعريف الأمبير بأنه 1 كولوم فى الثانية و أيضا **
كولوم = 6241418050180000000 إلكترون ( 6241 × 10^15 إلكترون )
من هنا نرى أن قانون أوم هو قانون بديهى مطبق فى كل جوانب الحياة تحت مسميات مختلفة
ف = ت × م أو V=I*R
هذا القانون يجب أن نشعر به و نتشربه لآن الكثير ممن عجزوا عن فهم أداء دائرة إلكترونية و تحليلها كان لخوفهم أن يطبقوا قانون أوم – أو فشلوا ظنا منهم أن دائرة بالدوائر المتكاملة لها قوانينها المتقدمة.
سينطبق قانون أوم فى بطارية ومقاومة كما سينطبق فى الميكرو ويف و خطوط نقل القدرة وعلى كل مستوى جزئى أو كلى أى جزء من الدائرة أو كلها أو بعضها.
أيضا السيد كيرشوف طبق هذا الكلام وسمى هذا التطبيق قانون كيرشوف الأول.
أيضا لا يوجد قانون كيرشوف ولكن هو من لاحظ تطبيق القانون الطبيعى فى الكهرباء.
ما هو؟ ببساطة تخيل مجموعة أصدقاء فى حلقة ساكنة ويشدوا بعض.
مادام لا حركة إذن هناك اتزان أى مجموع القوى متعادل أو = صفر
و السيد كيرشوف قالها بالكهرباء – ما دام هناك اتزان إذن مجموع القوى (الجهود أو الفولت) = صفر و الاتزان يطلب دائرة مغلقة لأن لو الحلقة فتحت تتحول لشد حبل وتكون هناك حركة.
هذا هو القانون الأول للسيد كيرشوف - ماذا عن القانون الثانى ؟
لو وقفت على باب و أخذت تعد الناس،
هل يصعب عليك أن تقول مادام لا يختفى البشر إذن عدد من دخلوا لا بد أن يساوى عدد من خرجوا – حسنا نسمه قانون باسمك كما سماه كيرشوف باسمه حيث قال:
مجموع التيارات الداخلة لأى نقطة = مجموع التيارات الخارجة منها
ملحوظة هامة جدا مرة أخرى : أنا لا أقلل من شأن أى من العلماء السابق ذكرهم فيكفيهم تقديرا أنهم لاحظوا ما لم يلاحظه غيرهم ولكن فقط أحاول تقليل الغموض حول الكهرباء والذى ينبت الخوف.
إن شئت أن تبنى حاسب ألى من مكوناته – تشرب بهذه القوانين الثلاث – أو إن شئت – قانون أوم و تطبيقيه كيرشوف 1 ، 2 و قاعدة ثيفينن.
مصادر الجهد والتيار موضوع الحلقة القادمة إن شاء الله

12

الآن وجب علينا أن نبدأ ببعض الدوائر
لنبدأ ببعض الدوائر يجب أن نضيف مصدر للتغذية – لذا نحتاج أن نعرف أنواع مصادر التغذية.
هناك نوعين فقط وكل نوع قد يعطى تيار مستمر أو متردد أو أى نوع آخر تريد – فقط نبدأ من البداية.
**النوعين هما مصدر جهد ثابت – و مصدر تيار ثابت **
طبعا ستطلب مثال ، قبل المثال نقول أنها مصادر غير موجودة فى الحياة لأنه لا يوجد شئ مثالى أو كامل لذا نجد أشياء أقرب ما تكون لذلك أو تتصرف هكذا فى حدود معينة – تقصد فى حمل معين ؟
حسنا لقد قلتها ولكن ما هو الحمل؟ الحمل هو التيار المسحوب من أى منها وليس المقاومة
لماذا اللعب بالألفاظ أليس الاثنان واحد؟
كلا فالحمل جزء منه هو المقاومة ولو كان شئ مثل الموتور مثلا فكيف سيكون الحال؟
– حسنا ما هى تلك المصادر؟
المصدر ذو الجهد الثابت : هو مصدر يعطى جهدا ثابتا "مهما كان الحمل أى مهما كان التيار"
إذن وضحت الصورة لماذا لا يمكن وجودة لأن مهما كان الحمل تعنى لو وضعنا قصر على مخرجه أى مقاومة = صفرا
بقانون أوم ف = ت × م إذن التيار = الجهد ÷ صفر أى = مالا نهاية !! وهو لا يمكن
لا تقل لماذا - فقط تذكر - كم مليون إلكترون لكل 1 أمبير والطاقة أيضا = الفولت × التيار = أيضا مالا نهاية!
لذا نكتفى بأن نقول أنه جهد ثابت على مدى حاجتنا
وهذا يتطلب أن تكون مقاومته الداخلية أصغر ما يمكن
هيه ما هذا الداخلية الذى تقول الآن
**مهلا فهو مكون من أسلاك توصيل و مكونات داخلية متنوعة وكل هذا له مقاومة مهما تكن صغيرة **
أمثلة البطاريات بأنواعها – مصادر التغذية عموما
النوع الثانى – مصادر التيار الثابت وهى من اسمها تعنى مصادر تعطى تيار ثابت بصرف النظر عن قيمة الحمل
و ماذا لو انقطع السلك ؟
طبعا لكى نمرر نفس التيار فى الهواء يجب أن نرفع الفولت لقيمة 20 ألف فولت لكل سم من المسافة بين طرفى السلك!
لذلك أيضا نكتفى أيضا بالقول أنه تيار ثابت فى نطاق احتياجاتنا
وهذا يتطلب أن تكون مقاومته الداخلية عالية جدا – مثال بعض دوائر شحن البطاريات تشحن بتيار ثابت
أيضا كما سنرى لاحقا الترانزستورات تعمل عمل مصدر تيار ثابت
وهذا رمز المصدرين المذكورين

المصدر الذى يغذى بجهد ثابت يرمز له برمز البطارية حيث كان أول اكتشافات واختراعات الكهرباء وكان له رمز مستقل ولما ظهرت مصادر الجهد المتردد ظهر لها رمز مستقل لكن مفهوم مصدر التيار الثابت لم يكن مستوعبا وقتها ، لذا نشأ الرمز متأخرا و مع التقدم العلمى رمز له بالحلقتين مع ذكر قيمة التيار و نوعه

هل طاقة المستمر تساوى طاقة المتردد؟
بالتأكيد تغير قيمة الجهد و من ثم التيار بالتبعية مع الزمن يجعل القدرة فى المتردد أقل منها فى المستمر المساوى له عدديا فى القيمة العظمى ، لذلك نشأت الحاجة لوحدة أخرى توحد آثار التيارين.
أخذ المتوسط لن يعطى الأثر المطلوب لأن القدرة تعتمد على حاصل ضرب التيار و الفولت، و بالنسبة للحمل ستكون مربع الفولت / المقاومة. بالتربيع سينتهى الجزء السالب من الموجة لأن -1-1=+1*
بأخذ متوسط الموجة الجديدة نحصل على مربع الطاقة المكافئة، و من ثم أخذ الجذر التربيعى لها يعطى هذه القيمة ولهذا سميت جذر متوسط التربيع RMS وهو جذر2 من القيمة العظمى أى قيمة القمة للموجة ألجيبية فقط و تختلف باختلاف شكل الموجة.

سنلاحظ من الرسم أن الجهد المتردد يتراوح ما بين قمة موجبة و مثلها سالبة وهذا يجعل القيمة بينهما أكبر، وهذا سيضع قيودا على تصميم المكبرات لاحقا. رجاء أن نتذكر أنه للحصول على 7 فولت متردد فهذه تعنى ج م ت **
** قمتها = 1.414 × 7 = 10 فولت و لحاجتنا إلى +10 و – 10 سنضطر لاستخدام مصدر تغذية 20 فولت على الأقل.

13

التوصيل على التوالى والتوازى

أولا نحاول تعريف هذا المفهوم
التوصيل على التوالى حين يخرج التيار بكامله من المكون الأول ليدخل بكامله إلى المكون الثانى.
التوصيل على التوازى حين يكون الجهد على المكون الأول بكامله على المكون الثانى.
أهمية هذا التعريف أننا حين نناقش الدوائر الإلكترونية لاحقا يظن البعض أنها على التوالى نظرا لكون خرج الدائرة الأولى يدخل الثانية وهذا فى الواقع له اسم خاص وهو التوصيل على التتابع لأن الدائرة الثانية تتبع الأولى أو تليها لكن لا يدخل تيار الأولى الدائرة الثانية بالمفهوم الذى شرحناه سابقا.
الآن سنطبق قانون أوم لتعرف تأثير توصيل المكونات على التوالى والتوازى و نأخذ الاعتبارات العملية بعد ذلك فهناك قليل من المفاجئات.
المقاومات:
المقاومة مثل سلك ملفوف أو قطعة من الكربون، عند توصيل أكثر من واحدة على التوالى كأننا أطلنا قطعة السلك أو يمكن القول أن من تعريف المقاومة
م = ρ × ل ÷ س حيث ρ هى المقاومة النوعية للمادة و ل = الطول بالسنتيمتر و س = مساحة مقطع السلك أو المادة
نجد أن من البديهى أن التوصيل على التوالى يعنى جمع هذه المقاومات.
م = م1 + م2 + م 3+ …

التوصيل على التوازى يوفر أكثر من مسار للتيار مما يجعل الحساب مطلوب
م = ف ÷ ت حيث ف= الفولت و ت = التيار و م= المقاومة المكافئة
بالنظر للمقاومات فى الرسم نجد

ت = ت1 + ت2 + ت3 + …
ت1 = ف ÷ م1
ت2 = ف ÷ م2 وهكذا و بالتعويض نجد

ت = ف/م1 + ف/م2 + ف/م3 +

بقسمة الطرفين على ف

ت/ف = 1/م = 1/م1 + 1/م2 + 1/م3 +…

أى أن مقلوب المقاومة المكافئة = مقلوب الأولى + مقلوب الثانية + الخ
من هذه العلاقة نجد أن س مقاومة على التوازى = قيمة الواحدة ÷ س
و مجموع مقاومتين على التوازى

م= م1*م2/ (م1+م2) أى حاصل الضرب مقسوما على ناتج الجمع.

أما القدرة بالوات فببساطة حاصل جمع القدرات، لكن هل تتحقق قاعدة القدرات عمليا ؟
فى التوصيل على التوالى يتوزع الجهد على المقاومات بنسب توازى قيمة كل منها، مما يجعل القدرة المستهلكة فى كل واحدة تتناسب مع ذلك الجهد و لهذا يجب أن نحترس ألا تصل إحداها لأكثر مما صممت لتحتمل.
مثال: هل توصيل مقاومة 100 أوم 1 وات على التوالى مع 10 أوم 1 وات يعطى 110 أوم 2 وات؟

القدرة = الفولت × التيار = الفولت × الفولت ÷ المقاومة = التيار × التيار × المقاومة
بالتطبيق على المقاومتين نجد أن
100 أوم تتحمل 0.1 أمبير
10 أوم تتحمل0.3162 أمبير
هكذا نرى أن عند تيار 0.1 أمبير، تصل الأولى لحدها الأقصى بينما تكون الثانية تتحمل 0.1 من قدرتها فقط و لو حاولنا زيادة التيار، ستحترق المقاومة الكبيرة فورا. الإجمالى فقط 1.1 وات وليس 2 وات.
أيضا فى التوصيل على التوازى يختلف التيار حسب قيمة المقاومات ويجب مراعاة نفس النقطة.
الصواب أن فى دوائر التوالى، نحدد التيار المطلوب، ثم نحسب لكل مقاومة القدرة التى تتحملها.
فى توصيل التوازى نحدد الجهد المفروض تواجده ثم نحسب لكل مقاومة القدرة التى تتحملها.

المكثفات:

هنا يجب أن نفرق بين قيمة المكثف والتى تعتمد على الجهد المتردد و بين تحمل المكثف للجهد المستمر
لنأخذ أولا مثال مكثف 0.1 مايكرو 50 فولت
ماذا تعنى القيمة 50 فولت؟ هل جهد مستمر أم أعلى جهد متردد أم ماذا؟
هذه القيمة تعنى أقصى فرق جهد كهربى يتحمله المكثف بأمان. هذا لا يعنى أن 51 سيدمر المكثف، وقد تقول أنك استخدمته مع 60 فولت ولم يحدث شيء.
معك كل الحق ولكن لنعرف القيم، لو كان صانع المكثفات يصنع 50 فولت و 100 فولت فهذا يعنى أن ما ينتجه من وحدات 50 فولت لا تتحمل 100 فولت ولكن هى بين 50 و أقل من 100 لهذا ليس من الحكمة أن نستخدمها مع جهد أعلى من 50 لأنها غير مأمونة.
من تعريف المكثف أنه لوحين بينهما عازل وقيمته تعتمد على مساحة اللوحين نجد أن التوصيل على التوازى يزيد من قيمة المكثف والسعة الكلية = المجموع
إذن س = س1 + س2 + س3 … الخ على التوازى
بتطبيق قانون أوم نجد أن على التوالى تصبح قيمة المكثف الكلية تخضع لقانون المقاومات على التوازى أى أن

س= 1/س1 + 1/س2 + 1/س3 + …

و كما قلنا فى مقاومات التوازى نقول لو وصلنا مثلا 5 مكثفات على التوالى متماثلة ستكون القيمة الكلية 1/5 قيمة الواحد
أى لو الواحد 0.1 مايكرو سيكون الخمسة تكافئ 0.02 مايكرو
الآن لماذا نوصل مكثفين على التوالى؟
طبعا ستقول لزيادة الفولت فمثلا أريد الحصول على مكثف 0.1 مايكرو يتحمل 1000 فولت و لدى مكثفات 200 فولت فأستخدم 5 قيمة كل منها 0.5 مايكرو فأحصل على 0.1 مايكرو 1000 فولت
لو كان الجهد متردد سيكون الكلام صحيحا 100% لكن لو كان الجهد مستمر مثل حالات مسدس الصعقة أو أى دائرة تعطى جهد مستمر عالى، سيختلف الأمر قليلا
هذه الدائرة نوصل فيها أربع مكثفات على التوالى و لهم نفس القيمة.
ما قيمة الجهود ف1 إلى ف4 بالفولت؟
طبعا ستقول 25 فولت!! لكن من أين جئنا بهذه القيمة؟

كجهد مستمر لبطارية فالتيار لا يمر و بالتالى لا يمكن أن يتجزأ حسب قانون أوم
ويمكن أن نحسن الموقف قليلا ونقول يتوزع حسب مقاومة التسريب لهذه المكثفات و التى نكون محظوظين لو كانت متقاربة، لذا سيكون على أحدها جهد أعلى مما يحتمل فينهار و يحدث به قصر فيلقى بالعبء على الباقى فينهار التالى وهكذا حتى ينهار الكل.
الحل أن نضع مقاومة كبيرة مثل 1 ميجا أو أعلى على التوازى مع كل مكثف تعمل كمنظم للجهد لكى يتوزع بالتساوى عليهم، وطبعا المقاومات تكون متساوية القيمة.
الموقف بالتأكيد سيكون أسوأ فى حال استخدام المكثفات الكيماوية بأنواعها .
لو استبدلنا المصدر المستمر بآخر متردد، فلاشك أن التقسيم سيكون صحيحا و الجهد المتردد سيتوزع بنسبة عكس قيم هذه المكثفات. أى أن المكثف الصغير تكون إعاقته كبيرة والجهد عليه أعلى من المكثف الكبير.

الملفات:

من طبيعة الملفات وكما فعلنا سابقا نجد أنها تشابه المقاومات و الحث الكلى يساوى مجموع حث الملفات عند التوصيل على التوالى و عند التوصيل على التوازى ينطبق قانون التوازى للمقاومات لكن هناك شرط
يجب ألا يرى أى من الملفات الباقى!! “يرى”؟؟ ما معنى هذا؟!!
الملف له مجال مغناطيسى وهذا يعنى ألا يؤثر مجال أى ملف على باقى الملفات وإلا سيصبح القانون معقدا لأنه يشمل نسبة تأثير كل ملف على الآخر حيث هنا نفكر فى محول وليس فى ملفات منفصلة.

لنجمع بعض المكونات المختلفة معا ونرى ماذا يكون – ربما مقاومة و مكثف أكثر تشويقا ،إذن سيكون ذلك موضوعنا القادم إن شاء الله.

إعجاب واحد (1)
14

دائرة المقاومة والمكثف

عند توصيلنا بطارية لدائرة مكونة من مقاومة و مكثف

فالجهد على المكثف = صفر و عليه فالتيار يكون مساويا قيمة البطارية V ÷ المقاومة R
لو تذكرنا ما قلنا فى آخر المشاركة الخاصة بالمكثفات عن السعة ! وهى = التيار × الزمن ÷ فرق الجهد
التيار ÷ فرق الجهد = 1 ÷ المقاومة
إذن السعة = الزمن ÷ المقاومة أو الزمن = المقاومة × السعة
T=RC
أليس هذا جميلا و بسيطا ؟ - لكن لماذا كانت هناك قوانين لوغاريتمية فى الموضوع؟
العلاقة الماضية صحيحة طالما كل متغيراتها تحافظ على قيمتها لنهاية القياس
أى نبدأ بتيار ما يظل ثابتا حتى نحصل على الزمن الذى نريده
و ما المشكلة؟
أن هذه الدائرة يجب أن تغذى من مصدر تيار ثابت لكن بالبطارية المذكورة و المقاومة تختلف الأمور

لو بدأنا بالأرقام : الفولت = 10 فولت والمقاومة 100 أوم و السعة 100000 ميكروفاراد (كبير قليلا لكن ليس مستحيلا)

إذن فرق الجهد الذى سيحدث = التيار × الزمن ÷ السعة
التيار = 10 ÷ 100 = 0.1 أمبير و الزمن واحد ثانية و السعة 0.1 فاراد
فرق الجهد = 0.1 × 1 ÷ 0.1 = 1 فولت
سنبدأ الثانية التالية و المكثف علية فولت كامل وهو سيطرح من جهد البطارية أى يتبقى 9 فولت
وعليه سيكون التيار أقل و يساوى 0.09 أمبير و يستطيع أن يضع شحنة أقل من السابقة فى ثانية فيكون للثانية رقم 2 فرق جهد أقل و على هذا نجد أن كل ثانية تضيف لجهد المكثف نسبه من الفولت أقل من سابقتها
متى يتم الشحن؟ ! لن يحدث

كيف؟ تخيل لديك تفاحة و كل ساعة تأخذ نصفها ستنتهى فى مرتين لكن تخيل أن كل مرة ستأخذ نصف ما تبقى ! متى ستنتهى؟ - لهذا تمام الشحن أو التفريغ فى مالا نهاية وهو طبعا غير عملى
لذا اتفق على أن يكون الحد هو 10% للتفريغ و 90% عند الشحن – فلو بدأ الشحن من الصفر فعند 90% أو فى المثال السابق 9 فولت نقول تم الشحن وهكذا و هذا أيضا له سبب عملى و منطقى وهو أننا لو طبقنا القوانين الدقيقة سنجد أنه يحدث عند خمسة أضعاف ضرب المقاومة فى المكثف أى
T=5RC
وهو رقم بسيط و سهل التذكر
أما بعد واحد R*C سيصل إلى 63% من قيمة الشحن
أرجو أن نلاحظ شيئا هاما هنا – نحن لا نتكلم عن قيمة البطارية حين نتحدث عن الشحن والتفريغ
هيه - أليست هى التى تشحن
نعم و لكن البطارية السابقة 10 فولت و تسبب 0.1 أمبير فى البداية للشحن إلى 10 فولت ، لو غيرنا البطارية بأخرى 20 فولت ستسبب تيار 0.2 للشحن أى سيكون أسرع ولكن للوصول لضعف الجهد ستأخذ ضعف التيار أو ضعف الزمن إذن لا تغيير .

يمكن إثبات هذا بالمعادلة ببساطة فالرسم يوضح معادلات الشحن والتفريغ لدائرة المقاومة والمكثف. هذه المعادلة يمكن كتابتها هكذا

حيث "“VC جهد المكثف عند أى لحظة ما ولتكن “ز” أو t” " و “Vcc” جهد البطارية و “هـ” هى أساس اللوغاريتم الطبيعى و قيمتها 2.718 و المقاومة والمكثف.
بقسمة الطرفين على Vcc أى ف تغذية:
ف مكثف / ف تغذية ستكون نسبة و بدون وحدات و تساوى القيمة بين القوسين وهى أيضا قيمة بدون وحدات.
إذن، زمن الوصول لنسبة ما لا يعتمد على قيمة البطارية بافتراض ثبوتها طوال زمن الشحن والتفريغ.

من هنا نجد أن للحصول على دقة زمن أعلى دوما يلجأ المصممون لنسبة من جهد البطارية بدلا من قيمة مطلقة – فلو دققت فى تفاصيل 555 الشهيرة تجد أنه يتعامل مع 1/3 ، 2/3 جهد البطارية و لا يستخدم زينر مثلا.

فى الرابط التالى شرح كامل بالمعادلات التى يصعب كتابتها لذا توضع صور.


هذا موقع جافا يقوم بحساباتها
http://www.phy.ntnu.edu.tw/ntnujava/index.php?topic=31
هل لو استخدمنا سلك بدلا من المكثف هل يكون هناك فرق؟ هو موضوع الحلقة القادمة إن شاء الله

15

دائرة المقاومة والملف

لماذا الملف – وهو قطعة من السلك – لا يتصرف كسلك عادى؟ أم السؤال معكوس و الأجدر أن نسأل هل السلك العادى يتصرف كملف مهما كان صغيرا؟
الإجابة هامة جدا حين نتعرض لفهم خطوط نقل القدرة وهو موضوع سلسلة مستقلة إن شاء الله
لو نظرنا فى الرابط التالى سنجد رسم الملف و المجال المتولد من لفة واحدة و حول سلك واحد و كيف يقطع باقى اللفات

http://www.ndt-ed.org/EducationResources/CommunityCollege/EddyCurrents/Physics/selfinductance.htm
لو فى حاجة لمراجعة المغناطيسية و المجال حول سلك الخ راجع نفس الموقع (الرابط التالى) لديهم منهج توضيحى مفيد
http://hyperphysics.phy-astr.gsu.edu/Hbase/electric/indcon.html#c1
من المفيد أن نأخذ المسألة خطوة بخطوة – الإلكترونات تدخل أول لفة ، لا تنسى أن الإلكترونات تعبر من مجال ذرة لأخرى فتولد مجال مغناطيسى يعبر الفضاء حوله و يقطع باقى أجزاء السلك مولدا فيه جهد ، وبما أنه رد فعل فلابد أن يكون معاكس لذا يسمى جهد عكسى Back EMF وهو يعاكس الجهد الأساسى و التيار الناتج منه وهذا ما يسمى بالحث الذاتى.
إذن الحث الذاتى خاصية لكل موصل سواء كان قطعة من سلك أو مقاومة أو مكثف أو كابل أو تراك (خط من النحاس) على بوردة

مما سبق نرى أن التيار لا يتمكن من الزيادة فجأة كما فى المكثف لا يمكن أن يزيد الجهد فجأة
المكثف كما قلنا أنه سعة مثل خزان لا يمكن ملؤه فجأة
والملف كالنابض (السوستة) لا يمكن ضغطها فجأة لا بد من زمن لقطع مسافة الضغط
لهذا فلو وصلنا مقاومة مع الملف سيسلك التيار فى الملف نفس سلوك الفولت فى المكثف
و بالتفصيل و القوانين فى الرابط التالى


قبل أن نغادر هذا المجال نريد توضيح بعض السلوك – ربما غير المتوقع

قلنا أن المكثف يشحن تدريجيا و يحتاج زمن لاكتمال الشحن و العامل الحاسم هنا هو المقاومة (لو فرضنا مكثف ما)
ماذا يحدث لو أصبحت المقاومة = صفرا؟
أعلم أنه لا توجد مقاومة = صفرا ولكن قطعة من السلك (قصر) مقاومته = مللى أوم أو ميكرو أوم
هيه - إذن لو كان المكثف مشحونا كالمثال السابق 10 فولت هل يسبب مثلا على ما تقول فى حال القصر مليون أمبير؟
الحمد لله أن لهذه القطعة من السلك حث ذاتى قد يؤخر نمو التيار ولو لميكرو ثانية قد تكفى لتفريغ المكثف
لهذا لو أخذت مكثف 1- 10 ميكرو مثلا لن يحدث مشكله أثناء تفريغه لكن لو كان 10000 ميكرو سترى له شرارة صغيرة، ولو أكبر والجهد أعلى قد يسبب التفريغ باستخدام مفك مثلا لحام المفك بطرف المكثف
وهذا الخطر يجب أن نحذره فى الدوائر الإلكترونية لأن مكثف 1000 ميكرو قد لا يسبب شرارة ترى ولكن بالتأكيد يتلف ترانزيستور لو تم التفريغ خلاله، كما أن نصفه مشحون بقيمة 300 فولت كما بوحدات التغذية الحديثة قد يسبب صدمة شديدة.

هذا عن المكثف – ماذا عن الملف !
نفس الكلام فقط نستبدل التيار بالجهد و القصر بالقطع فهما متعاكسان
لو أن التيار يمر فى ملف و يساوى مثلا أمبير واحد – ثم قطعنا التيار فجأة ، سيتوقف الإمداد بالتيار و يحاول المجال الذى مازال يولد الجهد العكسى فى توليده – إذن سيتولد جهد على أطراف الملف لا بد له أن يمر
كما حمدنا الله أن فى حال المكثف لقطعة السلك لها حث – نحمده الآن لأن بين أطراف الملف سعة فضلا على أن الهواء ليس عازلا مثاليا فعند بدء القطع ستكون المسافة ميكرو مترية يستطيع الجهد المتولد أن يعبرها فارضا تيارا معكوسا يفرغ هذا المجال الذى بنى حوله محدثا أيضا شرارة ذات جهد عالى كما كانت فى المكثف ذات تيار عالى.
أيضا لو كبر هذا الملف بالقدر الكافى قد تكون الشرارة مدمرة فهى تفرغ التيار فى مصابيح الفلوريسنت وهى السبب أن كل المفاتيح التى تتحكم فى موتورات تتعرض للشرار، بدء من موتور الخلاط وانتهاء بمحول الضغط العالى على أكبر محطة توليد
و بدون أن يكون كبيرا بالقدر الذى نظن – يكفى ملف تشغيل الريلاى يولد جهدا يكفى لتدمير الترانزيستور الذى يشغله
مبدأ عام فى كلاهما – ما يخزن عند البدء يفرغ لاحقا. شحنة المكثف أو مجال الملف

الملف و المكثف متعاكسان هل لو وصلناهما معا يلغى كل منهما الآخر؟
دوائر الرنين موضوع الحلقة القادمة إن شاء الله

إعجاب واحد (1)
16

دوائر الرنين

الرنين ظاهرة معروفة فى حياتنا عندما يتوفر شيئين يلغى تأثير أحدهما الأخر فتكون حالة تساوى الشيئين هى حالة رنين.
خواص حالة الرنين أنها تعمل عمل أشبه بالمكبر أو المعزز Booster وان كان هذا التشبيه خطأ ولكن يلجأ إليه المفسرون باعتبار أنه فجأة يختفى المجهود و يبدو أن الشىء يتصرف ذاتيا بسبب ميله الطبيعى للتصرف.
مثلا فى الميكانيكا الكتلة و الزنبرك حيث الكتلة توفر عزم القصور الذاتى أى تختزن الطاقة إن شئت أن تحركها و تعوقك إن شئت أن توقفها مثل الملف يعيق إدخال التيار إليه و بعد أن يمر يعيق إنقاصه – الزنبرك يخزن الطاقة فى صورة ضغط أشبه بالمكثف الذى تخزن الطاقة فى صورة ضغط (كلاهما قوة دافعة كهربية أو ميكانيكية)
عند تساوى القوتين يحدث الرنين حيث أقل قوة تعطى أكبر حركة و مثال الكوبرى الذى دمر من رتابة خطوة المشاة معروفة – أيضا الرنين فى الأصوات حيث يقوى الصوت عند تردد الرنين و ربما لن تصدق هذا، فالفرق بين الضوء العادى والليزر هو “الرنين”.
هذا الرابط يعطى تمثيلا بالصور على هذه الظاهرة
http://www.greenandwhite.net/~chbut/lc_oscillator.htm
كلنا نذكر توصيل المكثف بالبطارية ثم توصيل المكثف بالملف و تذبذب الطاقة بين المجال المغناطيسى فى الملف و الشحنة الكهربية فى المكثف.

نفترض أن المكثف مشحون بجهد 10 فولت. عند توصيله بالملف فالمفترض أن يمر تيار = مالا نهاية أى ∞ لأن مقاومة الملف نظريا = صفر ، وطبعا الملف لا يسمح بأن يزداد التيار فجأة من صفر لأى قيمة كانت بسبب ما ذكرناه عن الحث الذاتى و الجهد العكسى المتولد والذى يولد تيار عكسى.
أيضا المكثف من جهته لا يسمح بالتغير الفجائى للفولت من قيمة ما لقيمة أخرى فهو كالخزان يجب أن يملأ و يفرغ تدريجيا.
هكذا يجب أن يفرغ المكثف تدريجيا و يبنى الملف مجاله المغناطيس تدريجيا أيضا و بنفس المعدل و إلا، فأين سيذهب تفريغ المكثف الزائد عن طاقة بناء الملف للمجال؟؟ لا مسار لدينا.
هكذا يزداد التيار تدريجيا مع تفريغ المكثف و بناء المجال فى الملف، ما أن يمر تيار كافى لتساوى الجهدين على المكثف والملف، لا يستطيع المكثف أن يدفع مزيد من التيار فى الملف ولكن الملف لا يستطيع وقف التيار به مرة واحدة، فلو حاولت دفع عربه مشتريات فى سوق ثم أردت التوقف فجأة، لن تتركك العربة و ستجذبك هى ، وهذا ما يفعله الملف حتى يفرغ جهد المكثف تماما، فيتقلص المجال المغناطيسى و تتغلب القوة الدافعة العكسية فارضة استمرار التيار فى الاتجاه العكسى ليشحن المكثف تدريجيا أيضا و بنفس المعدل و إلا، فأين سيذهب تقلص المجال الزائد عن قدرة شحن المكثف ؟؟ لا مسار لدينا فيستمر هذا حتى يتم شحن المكثف بالقيمة السابقة بقطبية معكوسة، وهكذا تمت نصف دورة، لتعود و تتكرر بالقطبية الجديدة.
أرجو أن يكون مفهوم الرنين قد وضح، وهو ببساطة تساوى تبادل الطاقة بين المكثف و الملف.
**هنا يجب أن نشعر بأن هناك تردد واحد فقط يسمح بذلك و لا يجب أن تسأل ماذا لو لم تكن فى الرنين. السبب؟ هى الآن حرة الأداء فلن تعمل إلا عند تردد الرنين أما خارجه، فهذا يتطلب مصدر طاقه خارجى وهذا موضوع لاحق بإذن الله **

للأسف الحالة المثالية غير موجودة فالسلك له مقاومة أومية تحول بعض الطاقة لحرارة كما أن الملف لا يحتوى كل خطوط المجال و بعضها يفقد و المكثف أيضا لا يحتوى عازلا مثاليا فلهذا فبدلا من الاستمرار فى الاهتزاز لمالا نهاية ، تضمحل حتى تتلاشى.
طبعا كلنا نعلم التردد = 1 ÷ ( 2 × ط × جذر (ل×س)) كما هو مكتوب بالصورة السابقة
والمعادلة فى الموقع التالى
http://en.wikipedia.org/wiki/LC_circuit
**وعند حساب مقاومة السلك **
http://en.wikipedia.org/wiki/RLC_circuit
**الموقع التالى يقدم لك حسابات و رسم المنحنيات **
http://www.walter-fendt.de/ph11e/osccirc.htm
لكن هل هى متصلة على التوالى أم التوازى؟
توازى طبعا أليس الملف متصل بالمكثف؟
مهلا الإجابة ليست بهذه السهولة!
كيف؟ التيار يتبادل بينهما و الجهد واقع عليهما فلا نعرف كيف نحكم.
هذا موضوع الحلقة القادمة إن شاء الله

17

دوائر رنين التوالى و التوازى

من سيحكم إن كانت الدائرة توالى أم توازى؟
أنا؟ أنت؟ و ماذا نفعل بهذا؟ ما نريد هو سلوك الدائرة لنستخدمه وليس التعريف، إذن الحكم يكون لمن يتأثر تأثرا مباشرا بهذا السلوك و نكتفى نحن باستخدام النتائج أى مصدر التغذية.
إن كان المصدر على التوازى معهما كانت الدائرة – توازى
وإن كان المصدر على التوالى معهما كانت الدائرة – توالى
وهذا يشكل فارق أساسى قد تتوقف الدائرة بسببه عن العمل
كيف هذا؟!!

دائرة رنين التوازى:

فى دائرة التوازى ،كما نعلم، لو كان المصدر هو مصدر جهد ثابت ، إذن ستكون مقاومته الداخلية = صفرا أو أصغر ما يمكن
إذن لو غيرنا التردد من صفر – عبر الرنين – إلى أعلى ما يمكن (مالا نهاية) لن نجد فارق ، وهذا يتعارض مع أداء الدائرة التى نستخدمها فى فصل الترددات، أيضا - هناك نقطة أخرى أخطر وهى التيار الخارج من الملف ، هل يجد أفضل له أن يسير نحو المكثف أم يفرغ فى القصر الذى يفرضه المصدر؟

المصدر يضع قصرا على أطراف الدائرة و يلغى عملها لذا يجب وضعها مع مصدر تيار ثابت أو ذو مقاومة داخلية عالية لذا تجدها دائما مع ترانزيستور حيث يمثل المصدر المناسب فى دوائر المذبذبات.
أما عموما فتستخدم حيث تريد معاوقة (مقاومة) كبيرة عند التردد المعنى – و أقول المعنى و ليس المراد لأننا قد نريد التخلص منه فنمنع دخوله – الرابط التالى به معلومات أخرى
http://www.play-hookey.com/ac_theory/ac_lc_parallel.html

نلاحظ من دائرة الرنين أن جهد المنبع = جهد الملف = جهد المكثف ولكن بما أن التيار هنا يتبادل بين الملف و المكثف و عند الرنين لا يأتى من المصدر، إذن نلاحظ أن التيار فى كل منهما عالى جدا وهو يساوى Q من المرات أو سمها “ج” من المرات ما يأتى من المصدر. ج رمز لجودة الدائرة وهى Q رمز Quality Factor
ما الذى يجعله أكبر أو أقل؟
حسنا لو رجعنا للدائرة المرسومة نعرف أن الطاقة متبادلة بين الملف والمكثف و لو لم تفقد لكان تيار المصدر = صفر ولكن تياره يعوض الفقد فى دائرة الرنين وهو أساسا من ثلاث أسباب
1- مقاومة الملف الأومية وهى تفقد التيار فى صورة حرارة
2- فقد التسريب فى المكثف و باستخدام مكثفات ذات جودة عالية نقلل منه
3- فقد المجال المغناطيسى من واقع أن ليس كل المجال المتولد يبقى فى اللفات ولكنه يشع حولها ويمكن باستخدام قلب من مادة مغناطيسية مثل الفرايت ووضع عازل حوله تقليل هذا الفقد.
أكثرها تأثيرا هو مقاومة السلك وهو الذى يؤثر مباشرة على استجابة الدائرة ولهذا سميت النسبة السابقة Q أو ج معامل الجودة
ج = 2 ط ل / م حيث ط =3.14 و الحث ل و المقاومة م

  Q=ω  L / r

حيث ω = 2 π F
L = coil inductance
R coil’s wire resistance
المدى الذى تؤثر فيه دائرة الرنين كسائر المكبرات و الدوائر التى حسبنا لها نطاق ترددى تبنى على نظرية نصف الطاقة أى حيث يقل الجهد إلى 0.707 أو جذر2 من القيمة العظمى كما بالرسم وهو يتراوح بين قيمة صغرى و أخرى عظمى و تقل كثيرا خارجها
هذا النطاق الترددى = تردد الرنين ÷ معامل الجودة ج
∆f=fo/Q

حيث ∆f هو النطاق الترددى ، fo تردد الرنين
من معادلة الرنين أن التردد = 1 ÷ 2ط جذر ل س وأيضا حيث ω = 2 π F
ω = 2 π F = 1/جذر ل س
بالتعويض فى معامل الجودة ج
سنجد أن كلما زاد التردد قلت قيمة معامل الجودة وبالتالى لا نستطيع الحصول على ترددات ثابتة بسهولة
الآن لكى نحسب دائرة رنين توازى كحمل فى مكبر أو أى دائرة أخرى نجد أنها
المقاومة = ج × م حيث ج معامل الجودة و م مقاومة سلك الملف عند هذا التردد.
R=Q * r
هيه وما الفرق ، ألن تستمر فى الرنين و مقاومتها عند الرنين أعلى من الباقى؟
أجل ولكن سنحصل على انتقائية أقل – ماذا؟
سيكون فرق المقاومة بين ما نريد عند الرنين و خارج الرنين فرق صغير = Q من المرات و سيمر أكثر من تردد أيضا و بارتفاع التردد تزداد قيمة fo بينما تقل Q و بالتالى يتسع النطاق

لذلك في أجهزة الاستقبال يعتمد دوما على تحويل التردد لآخر منخفض لتحسين الانتقاء
لنتخيل معا – هل فتحت يوما تيونر (منتخب القنوات) لتلفاز من النوع القديم (يسمى دوار أو قلاب)
ستجد داخلة قرصين الأول مثبت عليه ملفات اختيار القناة و الثانى ملفات المذبذب المحلى و هو يختار القنوات 2 إلى 12 ،2-3-4 ذات تردد منخفض حوالى 50 ميجا ولكن من 5 إلى 12 تردداتها أعلى من 120 ميجا – لذا ملفاتها عبارة عن نصف لفة قطرها قرابة 5 مم فقط
أما قنوات التردد فوق العالى فتغيرت التقنية تماما
و فى ترددات المايكرو ويف نلجأ لتقنية ثالثة وهى الفجوات الرنانة

حسنا ماذا عن خارج تردد الرنين؟
بالطبع سنجد أن المعاوقة تقل حتى تصل تقريبا صفر عند تردد صفر و ∞ (مالا نهاية)
إذن ما يكون قصر عند تردد صفر هو الملف، أى أن
دائرة رنين التوازى تحت الرنين تكافئ حث تقل معاوقته تدريجا
أما أعلى من تردد الرنين فما يجعل المعاوقة = صفر عند تردد ∞ هو المكثف إذن
دائرة رنين التوازى فوق الرنين تكافئ سعة تقل معاوقتها تدريجا
دائرة التوالى الموضوع القادم إن شاء الله

إعجاب واحد (1)
18

دائرة رنين التوالى:

ماذا لو وضعنا المصدر على التوالى و أصبح لدينا دائرة توالى؟!
ببساطة لو وضعنا نفس المصدر السابق – مصدر تيار ذو معاوقة كبيرة – لن “يرى” كل من الملف والمكثف الآخر فسيعزل المصدر بينهما و لن يكون لدينا دائرة رنين .

لذا وجب أن نستخدم مصدر ذو مقاومة داخلية = صفرا أو أقل ما يمكن وهو مصدر جهد ثابت
عند الرنين كما عرفنا سابقا يتبادل المكثف و الملف الطاقة و طبعا يتسبب ذلك فى زيادة التيار زيادة كبيرة – لكن هناك كانت تمر خارج المصدر (توازى) أما هنا فستمر داخله – لذا وجب أن تكون مقاومته صغيرة
لذا عند الرنين يلاشى كل من الملف والمكثف الأخر و تصبح المقاومة = مقاومة السلك فقط
http://www.play-hookey.com/ac_theory/ac_lc_series.html
لذا تستخدم عندما نريد مقاومة صغيرة عند التردد المعنى.
أفضل استخداماتها فى المرشحات
لو لاحظنا الأداء سنجد تماثلا مع دائرة التوازى إلا أن الاختلاف نتج من حقيقة أين ننظر لها ، هل من خارجها موازيين لها أم من داخلها.
لذا فنفس قوانين الرنين ومعامل الجودة مطبقة فقط ندرك أن المقاومة عند الرنين ستكون صفر أو أصغر ما يمكن و من الحوار السابق فى رنين التوازى ندرك أنها ستكون قيمة مقاومة سلك الملف عند هذا التردد.
أيضا النطاق الترددى مبنى على 0.707 من القيمة الصغرى ونفس القانون.
الآن نفس تيار المصدر يمر فى كل من الملف والمكثف، لكن الجهد هنا أحدهما يسبق بقيمة 90 درجة و الآخر يتأخر بمقدار 90 درجة مما يجعل مجموعهما = صفر لكن لكل منهما قيمة = حصل ضرب معامل الجودة فى جهد المصدر.
ربما كان لديك دائرة رنين توالى تعمل على تغذية 15 فولت و كان المكثف 200 فولت ثم استبدلته بآخر 50 ظنا أنه أعلى من التغذية بكثير ولكنه لم يحتمل. السبب أن معامل الجودة 20 و المصدر (المهتز) يعطى 5 فولت و علية سيكون على المكثف جهد = 20 × 5 = 100 فولت. مفاجئة!!!

عند الرنين كما علمنا وتوقعنا الدائرة تكافئ مقاومة لكن عند تردد ∞ و تردد صفر المعاوقة تكاد تكون مالا نهاية أيضا، و عند تردد صفر المكثف هو ما يجعل دائرتها مفتوحة إذن
دائرة رنين التوالى تحت الرنين تكافئ سعة تزيد معاوقتها تدريجا
أما فوق الرنين فالملف هو ما يجعل معاوقتها تزيد إذن
دائرة رنين التوالى فوق الرنين تكافئ حث تزيد معاوقته تدريجا

هيه تقول مقاومة الرنين – أين الملف والمكثف؟
كما علمنا أن عند تردد الرنين يلاشى كل من الملف والمكثف بعضهما البعض و تبقى مقاومة السلك

و ما قصة مقاومة سلك الملف عند التردد المعنى؟؟
مقاومة السلك كما نعلم تعتمد على الطول و المادة و مساحة المقطع
هناك ظاهرة تسمى تأثير السطح Skin Effect وهى أن التيار المستمر يعبر السلك فى كامل مساحة مقطعة، لكن عند ظهور تردد ، هذا لحظيا يجعل المجال المغناطيسى يزداد و يتقلص مولدا تيارات تأثيرية معارضة تقلل من التيار المار فى منتصف السلك وهذا يسبب تقليل مساحة المقطع الفعلية.
هل سألت نفسك مرة لماذا كل هوائيات التلفاز تصنع من مواسير من الألمونيوم و ليست قضبان ؟ لأن مادة القلب فعلا لا يمر فيها تيار.
كلما ارتفع التردد قل سمك الطبقة التى يمر فيها التيار حتى أنك تجد من المنحنيات المقابلة عند تردد 1 ميجا سيكون سمك الطبقة من النحاس التى يمر فيها التيار أقل من 0.1 مم


رابط لحاسبة تحسب لك سمك هذه الخاصية
http://daycounter.com/Calculators/SkinEffect/Skin-Effect-Calculator.phtml
http://www.microwaves101.com/encyclopedia/calsdepth.cfm
http://www.calculatoredge.com/electronics/skin%20effect.htm

المرة القادمة إن شاء الله نحلل الدوائر الأكثر تعقيدا.

19

نظرية ثيفينن Thevenin’s theorem

بالطبع ستسألنى "لقد تعلمت فى الإنجليزية أن نظرية تعنى Theory وهى كذلك دوما إلا فى ثيفينن، لماذا؟ " هل لأنه أسماها هكذا؟؟
كلمة Theory تعنى نظريه وهى لم ترتقى بعد لمرتبة القانون و يمكن دحضها و مناقشتها و إثبات صوابها أو خطؤها أو الاثنان معا فهى من وجهة نظر صائبة و من وجهة نظر أخرى خاطئة. و مقابلها “قانون”.
أما كلمة theorem فهى تعنى تناول حقيقة علمية عملية من الجانب النظرى لها وهى صحيحة لكونها مبنية على قانون أو مجموعة قوانين، وهى مثبت صحتها ولا تدحض. و مقابلها هو التناول العملى المعملى للقضية. وللأسف ليس لها ترجمة بالعربية.
كل ما يخص هذه النظرية يتصل بالعناصر الخطية فقط مثل المقاومات والمكثفات والملفات
ولو لدى دائرة بها ثنائى أو ترانزيستور مثلا ماذا أفعل؟!!
هناك ثلاث حلول لهذه المسألة،
1- نعتبر تطبيق القوانين فى نطاق التغيير المحدود حيث يمكن اعتبار هذا العنصر خلالها خطيا
2- نرفع العنصر إن أمكن و نستبدل الدائرة بمكافئها.
3- أخيرا نستبدل العنصر بدائرة تماثل أو تقارب استجابة العنصر، مثلا الثنائى يمثل بمقاومة كبيرة تحت 0.6 فولت و أخرى صغيرة فوق 0.6 فولت ولا مانع من وضع ثنائيات مثالية تكون إما قصر أو مفتوح.

القاعدة الأولى هى تحويل مصدر الجهد لمصدر تيار والعكس

فى هذا الرسم نجد أن المصدر المثالى له مقاومة = صفر مما يجعل التيار ∞ وهذا يجعل التطبيق مستحيل لأنه سيستخدم علاقات مثل 0 × ∞ = ؟ ، ولهذا نستخدم المصادر العملية المتواجدة فى الطبيعة.

هذا الرسم يوضح القاعدة الأولى وهى أن مصدر الجهد الثابت (سواء مستمر أم متردد) يمكن أن يستبدل بمصدر تيار ثابت، قيمته تساوى قيمة تيار القصر Short Circuit current لمصدر الجهد و على التوازى معه مقاومة تساوى مقاومة مصدر الجهد الداخلية.
أى أن التيار = الفولت ÷ المقاومة
والعكس بالعكس. أى أن مصدر الجهد = التيار × المقاومة.
نلاحظ أن كلتا الدائرتين لهما نفس المقاومة المكافئة بين الطرفين فلأن مصدر التيار مقاومته ∞ تكون المقاومة بين الطرفين هى R و مصدر الجهد الثابت مقاومته الداخلية = 0 إذن المقاومة بين الطرفين أيضا هى R
يمكننا أن نستغل هذا التحويل لإيجاد مكافئ لدائرة معقدة حيث نبدأ بمصدر الجهد و نجمع مع مقاومته الداخلية كل المقاومات على التوالى ثم نحوله لمصدر تيار لنجمع المقاومات على التوازى ثم عودة للتوالى ثم التوازى وهكذا.
غالبية الدوائر تحتوى أكثر من مصدر لذا يصعب إتباع هذا النهج دوما وهو ما يقودنا للقانون الثانى.

لصق الصورة 745×152 2.98 KB

قانون ثيفينن الثانى يقول أنه فى أى دائرة يكون التيار المار فى أى فرع مساويا مجموع التيارات الناتجة من كل مصدر على حده باعتبار استبدال باقى المصادر بمكافئاتها.
وهذا بديهى، فلو شخص ما يعانى وهو يحاول دفع عربة مثلا ، ستقول أحضروا شخصا يساعده، أى أنك تقر أن تأثير الاثنان هو مجموع تأثير الأول مع تأثير الثانى وهذا ما قاله ثيفينن فى التيار.
مثلا فى الدائرة السابقة يكون التيار المار مثلا فى Rld مساويا مجموع التيار الناتج من V1 مع استبدال V2 بقصر كما بالرسم و التيار الناتج من V2 مع استبدال V1 بقصر كما بالرسم.
حسنا وماذا عن الفولت؟؟
نفس القاعدة مطبقة عن الفولت.
لمعرفة ماذا يواجه الحمل Rld يمكننا أن نرفع الحمل من الدائرة و نحسب الجهد الموجود على أطرافه، ثم ننظر من خلال أطراف الحمل لباقى الدائرة بعد استبدال المصادر بمكافئاتها من المقاومات كما يلى

لنحسب الجهد الناتج من المصدر الأول سيكون 60 × 40 / (40+20)
ف 1 = 60 × 40 / 60 = 40 فولت وهو مرسوم فى دائرة المحصلة.
ف2 = 30 × 20 / (20+40) = 30 × 20 / 60 = 10 فولت
إذن المحصلة = 40 فولت + 10 فولت. لو المصدرين من نفس النوع يمكننا القول = 50 فولت و هنا استخدمت مصدر مستمر و آخر متردد لتوضيح فكرة الجمع والإضافة.
لحساب المقاومة المكافئة سنضع قصرا على المصدرين فنجد أن المكافئ هو R1 بين الطرف العلوى و السفلى جهة V1 على التوازى مع R2 بين الطرف العلوى و السفلى من جهة V2 و لكن R3 ستكون بين الأرضى من جهة V1 والأرضى من جهة V2 أى كما أن عليها قصر. ولو نظرت للدائرة الأساسية، ستجد فعلا أن R3 ل دخل لها فى الحمل إطلاقا. و من ثم 20//40 = 13.33 وهذا هو المكافئ و بتوصيل الحمل نحسب ما نريد.
بهذه القواعد نستطيع تبسيط أى دائرة معقدة لدائرة بسيطة يسهل التعامل معها.

أشباه الموصلات موضوع الحلقة القادمة إن شاء الله

20

أشباه الموصلات Semi-Conductors

تنقسم المواد إلى مواد موصلة وهى ذات مقاومة نوعية ρ أقل من حد معين و مواد عازلة ذات مقاومة نوعية ρ أعلى من قيمة معينة و بينهما منطقة حيث ρ فيها لا تناسب التوصيل ولا العزل ، لذا تسمى أشباه الموصلات. لا استخدم تعبير “أنصاف الموصلات” لأن النصف عدد ذو قيمة و موصل له نصف توصيل النحاس سيظل موصلا أيضا.
ماذا يكون التعريف الأنسب إذن؟
لو نأخذ التقسيم السابق من حيث التركيب الذرى سنحدد تعريفا جيدا لأشباه الموصلات. ما يلى بالغ الأهمية لفهم أشباه الموصلات بأنواعها لأن الكثير يخلط بين النوع س أو N وكونه سالب أو متعادل و بالمثل فى النوع م أو P .

تتركب المواد من جزيئات تحتوى ذرات. كل ذرة تتركب من نواه بها عدد من البروتونات الموجبة والنيوترونات المتعادلة ، عدد البروتونات يحدد العنصر و خواصه إذ لا يوجد عنصرين لهما نفس العدد.
عدد البروتونات يمثل شحنة موجبة، ولابد لهذه الشحنة من أن تتعادل فتجذب إليها إلكترونات سالبة تدور فى مسارات حول النواة و كل مسار له عدد محدد من الإلكترونات لا يتغير ما عدا المدار الأخير الأبعد عن النواة.
هذا المدار الأخير يتسع لثمانى الكترونات فقط ولكن عدد البروتونات قد لا يجذب ما يكفى لإكمال هذا المدار الأخير، هذا الوضع يخلق حالة عدم استقرار للنوة، تريد إكمال المدار الخارجى ليحتوى ثمانية الكترونات ولا تريد زيادة الشحنة السالبة عن الشحنة الموجبة، ولم يخلق الله الكترونات متعادلة!! إذن ما الحل؟

الحل أن ترتبط الذرات معا ، كيف ؟!! حسنا لننظر للتركيب
المدار الأخير يريد ثمان الكترونات لهذا فالرقم السحري هو نصفه أى 4
ما هذا الرقم السحرى؟

ترتبط الذرة مع الأربع ذرات المحيطة معا بحيث كل إلكترون من هذه الذرة يرتبط مع إلكترون من ذرة مجاورة فكأنهما يدوران فى فلك هذه الذرة معا وتلك الذرة معا فتكون كل الذرات كما لو أن مدارها الخارجى مكتمل بثمانى الكترونات.

نلاحظ هنا نوعين من الارتباط
ارتباط كيمائى وهو التكافؤ الرباعى واكتماله بتحقيق 8 الكترونات فى المدار الخارجى.
ارتباط كهربى و تحققه بأن عدد الإلكترونات مساوى لعدد البروتونات ولا توجد شحنات زائدة.
نتيجة الارتباط الوثيق بين الإلكترونات و النواة، لا نجد كثير من الإلكترونات الحرة وهى التى تسبب مرور التيار.
من أمثلتها الكربون النقى و الجرمانيوم النقى و السليكون النقى.
ماذا نفعل إذن لنزيد التوصيل؟
الحل ببساطة أن نضيف قليلا من الشوائب، ولا نقصد مواد رديئة ولكن نقصد عناصر أخرى.
آه ، إذن هذه العناصر هى التى توصل التيار فى المادة شبه الموصلة!!
لا، ولكنها فقط توفر آلية النقل.
ولماذا إذن هذا العذاب ولدينا الأفضل مثل النحاس والمعادن كلها.

الفكرة أننا لا نسعى للتوصيل ولكن نسعى لخلق اختلال فى التكوين يهيئ لنا أن نستغله فى هذا العالم الكبير – عالم أشباه الموصلات.

لو وضعنا قليلا من عنصر خماسى التكافؤ – هذا يعنى أن لمداره الخارجى خمسة إلكترونات. إذن ستشترك أربع منها مع ذرات السيلكون كما سبق ويبقى الخامس بدون ارتباط، وهذا يشرح آلية النقل حيث كان العنصر الخماسى قبل المزج يقال عنه “الكترونات المدار الخارجى حرة” و الآن واحد فقط حر.

لاحظ هنا الاختلال الحادث، هذا الإلكترون لا يمكنه البقاء لأن لا ارتباط له مع ذرة مجاورة . حسنا ليمضى لحال سبيله!!

إلى أين يمضى وهو مقيد بالبروتون الموجب المناظر له فى ذرته!
موقف غريب قليلا ولكنه ذو فائدة جليلة. هذا الإلكترون حر الحركة لكن يجب أن يأتى بديله حتى تتعادل شحنات الذرات وهكذا يكون لدينا إمكانية نقل التيار بهذه الإلكترونات الحرة و لهذا سميت المادة “سالبة” وإن كانت ليست سالبة الجهد أو الشحنة ولكن ما ينقل التيار فيها هو الإلكترونات السالبة.

تذكر هذا جيدا أن المادة متعادلة كهربيا ولكن بها إلكترونات حرة كثيرة قابلة للحركة. أى أن الوسيط لنقل التيار هو إلكترونات سالبة الشحنة.

الآن ماذا لو وضعنا مادة ثلاثية التكافؤ؟ تذكر أن ثلاثية التكافؤ تعنى مدارها الخارجى يحتوى ثلاث ذرات.
نفس القضية إلا أن لدينا الآن ثلاث الكترونات فقط وهذا سيخلق وضعا غريبا أيضا .
ترتبط الإلكترونات الثلاث بثلاث ذرات مجاورة والرابعة لن تجد إلكترون يحقق لها رابطة التكافؤ. ولكن التعادل الكهربى محقق.

هذا سيخلق نقصا أو فجوة أو مكان يمكن لأى إلكترون عابر أن يسقط فيه ليحقق رابط التكافؤ ولكن، عند حدوث هذا سيختل التعادل الكهربى و تصبح الشحنات السالبة أكثر من الموجبة، لهذا يمكن لهذا الإلكترون أن يلفظ منتقلا إلى ذرة مجاورة بها فجوة أيضا وهو ما يبدو كأن الفجوة انتقلت فى الجهة المضادة ، و أؤكد هنا ما يبدو لأن من انتقل فعليا هو الإلكترون وهو الجسيم ذو الكتلة وهو الذى يمكن أن يوجد فى حالة منفصلة و يتحرك فى الفراغ لكن لا يوجد جسم اسمه فجوة ولا يوجد فى الفراغ ولا يوجد خارج هذا التكوين الذرى.
لتسهيل الحوار اعتبر العلماء أن الفجوة موجبة لكونها تجذب إلكترون سالب و هى تتحرك عكس الإلكترون أخذا فى الاعتبار أن التفصيل الدقيق تم فهمة و سميت المادة موجبة م P على اعتبار أن الفجوات هى ناقل التيار مجازا.
المسألة أشبه عندما نبيع عقار عليه دين بقولك انتقل الدين من س إلى ص بينما فى الحقيقة ما انتقل هو المال من ص إلى س.

مما سبق نستخلص حقيقة أن دوما انتقال التيار فى المادة س أو N أسرع من انتقاله فى المادة م أو P والسبب أن انتقال الإلكترون مباشرة من ذرة لأخرى دوما سيكون أسرع من انتقال الفجوة والرسم المقابل يشرح لماذا.

هل ستجد حركة الإلكترون بالطريقة العليا أسرع أم انتقاله للفجوة ثم انتقال التالى للفجوة الجديدة ثم التالى فالتالى!!

الآن ماذا يحدث لو التحمت وصلتان م و س أو P,N معا؟

هذا موضوع المرة القادمة إن شاء الله

إعجاب واحد (1)